题目内容
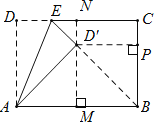
【题目】如图,在矩形ABCD中,AD=10,AB=14,点E为DC上一个动点,若将△ADE沿AE折叠,当点D的对应点D′落在∠ABC的角平分线上时,则点D′到AB的距离为( )

A. 6 B. 6或8 C. 7或8 D. 6或7
【答案】B
【解析】分析:连接BD′,过D′作MN⊥AB,交AB于点M,CD于点N,作D′P⊥BC交BC于点P,利用勾股定理求出MD′.
详解:∵点D的对应点D′落在∠ABC的角平分线上, ∴MD′=PD′,
设MD′=x,则PD′=BM=x, ∴AM=AB-BM= 14-x,
又折叠图形可得AD=AD′=10, ∴x2+(14-x)2=100,解得x=6或8,即MD′=6或8.
即点D′到AB的距离为6或8,故选B.

练习册系列答案
相关题目
【题目】某工厂一周计划每日生产某产品100吨,实际每日生产量与计划量相比情况如下表(以计划量为标准,增加的吨数记为“+”,减少的吨数记为“﹣”)
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减/吨 | ﹣1 | +3 | ﹣2 | +4 | +7 | ﹣7 | ﹣11 |
(1)生产量最多的一天比生产量最少的一天多生产多少吨?
(2)若本周总生产的产品全部由35辆货车一次性装载运输离开工厂,则平均每辆货车大约需装载多少吨?