Question

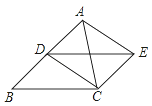
【题目】已知，如图，点D是△ABC的边AB的中点，四边形BCED是平行四边形，

（1）求证：四边形ADCE是平行四边形；

（2）当△ABC满足什么条件时，平行四边形ADCE是矩形？

Answer 1

【答案】见解析

【解析】试题分析：证明是平行四边形的方法有很多，此题用一组对边平行且相等较为简单，在平行四边形的基础上只需一个角是直角即可．

试题解析：证明：（1）∵四边形BCED是平行四边形，∴BD=CE且BD∥CE．又∵D是△ABC的边AB的中点，∴AD=BD，即DA=CE．又∵DA∥CE，∴四边形ADCE是平行四边形．

（2）当△ABC为等腰三角形且AC=BC时，四边形ADCE是矩形．证明如下：

∵AC=BC，D是△ABC的边AB的中点，∴CD⊥AD，∴∠CDA=90°．∵四边形ADCE是平行四边形，∴四边形ADCE是矩形．