题目内容
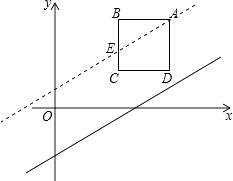
【题目】如图,在平面直角坐标系中,边长为2的正方形ABCD在第一象限内,AB∥x轴,点A的坐标为(5,3),己知直线l:y= ![]() x﹣2
x﹣2 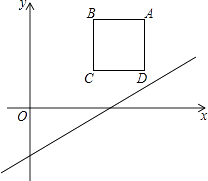
(1)将直线l向上平移m个单位,使平移后的直线恰好经过点A,求m的值
(2)在(1)的条件下,平移后的直线与正方形的边长BC交于点E,求△ABE的面积.
【答案】
(1)解:设平移后的直线方程为y= ![]() x+b,
x+b,
把点A的坐标为(5,3)代入,得
3= ![]() ×5+b,
×5+b,
解得 b= ![]() .
.
则平移后的直线方程为:y= ![]() x+
x+ ![]() .
.
则﹣2+m= ![]() ,
,
解得 m= ![]()
(2)解:∵正方形ABCD的边长为2,且点A的坐标为(5,3),
∴B(3,3).
把x=3代入y= ![]() x+
x+ ![]() ,得
,得
y= ![]() ×3+
×3+ ![]() =2,
=2,
即E(3,2).
∴BE=3﹣2=1,
∴△ABE的面积= ![]() ×2×1=1.
×2×1=1.
【解析】(1)直线平移,斜率不变,设平移后的直线方程为y= ![]() x+b;把点A的坐标代入进行解答即可;(2)根据平行后的直线方程和直线x=3来求点E的坐标,然后利用三角形的面积公式进行解答.
x+b;把点A的坐标代入进行解答即可;(2)根据平行后的直线方程和直线x=3来求点E的坐标,然后利用三角形的面积公式进行解答.

练习册系列答案
相关题目