题目内容
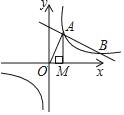
【题目】如图,已知AB⊥BC,CD⊥BC,AB=4,CD=2.P为线段BC上的点,设BC=m.
⑴若m=9,
①若△BAP∽△CDP,求线段BP的长;
②若△BAP∽△CPD,求线段BP的长;
⑵试求m为何值时,使得△BAP与△CDP相似的点P有且只有2个.

【答案】(1)①6;②8或1;(2)m=6或4![]()
【解析】
(1)根据相似三角形的性质即可得到结论;
(2)①当△BAP与△CDP都是等腰直角三角形时,两三角形相似,于是得到结果;
②当根据相似三角形的性质和一元二次方程根的判别式即可得到结论.
(1)∵BC=9,∴PC=9﹣BP.
①∵△BAP∽△CDP,∴![]() ,即
,即![]() ,解得:BP=6;
,解得:BP=6;
②∵△BAP∽△CPD,∴![]() ,即
,即![]() ,解得:BP=8或1;
,解得:BP=8或1;
(2)①当△BAP与△CDP都是等腰直角三角形时,两三角形相似,此时∠BPA=∠CPD=45°,则BP+PC=BC=AB+CD=6;
②当∠BAP=∠CPD时,△BAP∽△CPD,∴![]() ,即
,即![]() ,∴BP2﹣mBP+8=0,∴△=m2﹣32=0,∴m=±4
,∴BP2﹣mBP+8=0,∴△=m2﹣32=0,∴m=±4![]() (负值舍去),∴m=4
(负值舍去),∴m=4![]() .
.
综上所述:当m=6或4![]() 时,△BAP与△CDP相似的点P有且只有2个.
时,△BAP与△CDP相似的点P有且只有2个.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
【题目】小冬与小夏是某中学篮球队的队员,在最近五场球赛中的得分如下表所示:
第一场 | 第二场 | 第三场 | 第四场 | 第五场 | |
小冬 | 10 | 13 | 9 | 8 | 10 |
小夏 | 12 | 2 | 13 | 21 | 2 |
(1)根据上表所给的数据,填写下表:
平均数 | 中位数 | 众数 | 方差 | |
小冬 | 10 | 10 | 2.8 | |
小夏 | 10 | 12 | 32.4 |
(2)根据以上信息,若教练选择小冬参加下一场比赛,教练的理由是什么?
(3)若小冬的下一场球赛得分是11分,则在小冬得分的四个统计量中(平均数、中位数、众数与方差)哪些发生了改变,改变后是变大还是变小?(只要回答是“变大”或“变小”)
(![]() )
)