Question

【题目】如图，在四边形ABCD中，AB=AD=4，∠A=60°，BC=4 ，CD=8．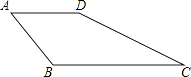
（1）求∠ADC的度数；
（2）求四边形ABCD的面积．

Answer 1

【答案】
（1）解：连接BD，

∵AB=AD，∠A=60°，

∴△ABD是等边三角形，

∴∠ADB=60°，DB=4，

∵42+82=（4 ）2，

∴DB2+CD2=BC2，

∴∠BDC=90°，

∴∠ADC=60°+90°=150°

（2）解：过B作BE⊥AD，

∵∠A=60°，AB=4，

∴BE=ABsin60°=4× =2 ，

∴四边形ABCD的面积为： ADEB+ DBCD= ×4× + ×4×8=4 +16

【解析】（1）连接BD，首先证明△ABD是等边三角形，可得∠ADB=60°，DB=4，再利用勾股定理逆定理证明△BDC是直角三角形，进而可得答案；（2）过B作BE⊥AD，利用三角形函数计算出BE长，再利用△ABD的面积加上△BDC的面积可得四边形ABCD的面积．
【考点精析】关于本题考查的勾股定理的逆定理，需要了解如果三角形的三边长a、b、c有下面关系：a2+b2=c2，那么这个三角形是直角三角形才能得出正确答案．