题目内容
已知直线y=kx-4(k>0)与x轴和y轴分别交于A、C两点;开口向上的抛物线y=ax2+bx+c过A、C两点,且与x轴交于另一点B.(1)如果A、B两点到原点O的距离AO、BO满足AO=3BO,点B到直线AC的距离等于
| 16 | 5 |
(2)问是否存在这样的抛物线,使得tan∠ACB=2,且△ABC的外接圆截y轴所得的弦长等于5?若存在,求出这样的抛物线的解析式;若不存在,请说明理由.
分析:(1)本题可通过构建直角三角形求解,过B作BE⊥AC于E,交y轴于D,可根据直线的解析式用k表示出OA、OB的长,即可得出AB的长,已知了BE的长度,可用勾股定理求出AE的长;
AE长的另一种表示方法:在直角三角形ABE中,∠BAE的正弦值正好是斜率k,因此可用∠BAE的正弦值即k和BE的长表示出AE,然后联立两个AE的表达式即可求出k的值.进而可求出直线的解析式和抛物线的解析式.
(2)已知了C点坐标,关键是确定抛物线的二次项系数和一次项系数.可用韦达定理来求解.已知了三角形ABC的外接圆(设圆心为P)截y轴的弦长为5,那么OD=1,根据相交弦定理可求出OA•OB的值,即可得出韦达定理中两根积的值,即可求出二次项系数的值.连AP、BP,过P作PE⊥x轴于E,PF⊥y轴于F.
根据垂径定理和圆周角定理不难得出∠ACB=∠APE,那么tan∠APE=2,据此可求出AE和AB的长,即可得出A、B横坐标差的绝对值,由此可求出一次项系数的值,即可确定抛物线的解析式.
AE长的另一种表示方法:在直角三角形ABE中,∠BAE的正弦值正好是斜率k,因此可用∠BAE的正弦值即k和BE的长表示出AE,然后联立两个AE的表达式即可求出k的值.进而可求出直线的解析式和抛物线的解析式.
(2)已知了C点坐标,关键是确定抛物线的二次项系数和一次项系数.可用韦达定理来求解.已知了三角形ABC的外接圆(设圆心为P)截y轴的弦长为5,那么OD=1,根据相交弦定理可求出OA•OB的值,即可得出韦达定理中两根积的值,即可求出二次项系数的值.连AP、BP,过P作PE⊥x轴于E,PF⊥y轴于F.
根据垂径定理和圆周角定理不难得出∠ACB=∠APE,那么tan∠APE=2,据此可求出AE和AB的长,即可得出A、B横坐标差的绝对值,由此可求出一次项系数的值,即可确定抛物线的解析式.
解答: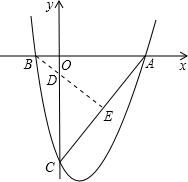 解:(1)易知:A(
解:(1)易知:A(
,0),
因此OA=
,OB=
,B(-
,0),
∴AB=
,
过B作BE⊥AC于E,交y轴于D,在直角三角形ABE中,
AE=
=
.
根据直线AC的斜率可知:直角三角形ABE中,tan∠BAE=k,
因此AE=
=
,即:
=
,
解得k=
(负值舍去).
∴直线的解析式为y=
x-4.
∴A(3,0),B(-1,0)
设抛物线的解析式为y=a(x-3)(x+1),
由于抛物线过C(0,-4),
则有:a(0-3)(0+1)=-4,a=
,
∴抛物线的解析式为y=
x2-
x-4.
(2)假设存在这样的抛物线,其解析式为y=ax2+bx-4.
设△ABC的外接圆圆心为P,连AP、BP,过P作PE⊥x轴于E,PF⊥y轴于F.
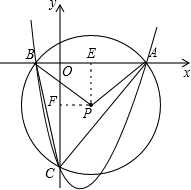 ∵圆P截y轴所得弦长为5,且过点A、B及C(0,-4).
∵圆P截y轴所得弦长为5,且过点A、B及C(0,-4).
∴圆P过点D(0,1)
∴P点在x轴下方,
∴CF=DF=
,PE=OF=4-
=
.
∵∠APE=
∠APB=∠ACB,
∴tan∠APE=
=tan∠ACB=2,
∴AE=2PE=3,
∴AB=2AE=6,
∵OA•OB=OC•OD,即-x1x2=4.
∴
=4,a=1.
∴抛物线的解析式为y=x2+bx-4.
∵AB=6,
∴x1-x2=6.
∴(x1-x2)2=(x1+x2)2-4x1x2=b2+16=36.
∴b=±2
.
∴存在这样的抛物线y=x2±2
x-4.
 解:(1)易知:A(
解:(1)易知:A(| 4 |
| k |
因此OA=
| 4 |
| k |
| 4 |
| 3k |
| 4 |
| 3k |
∴AB=
| 16 |
| 3k |
过B作BE⊥AC于E,交y轴于D,在直角三角形ABE中,
AE=
| AB2-BE2 |
(
|
根据直线AC的斜率可知:直角三角形ABE中,tan∠BAE=k,
因此AE=
| BE |
| k |
| 16 |
| 5k |
(
|
| 16 |
| 5k |
解得k=
| 4 |
| 3 |
∴直线的解析式为y=
| 4 |
| 3 |
∴A(3,0),B(-1,0)
设抛物线的解析式为y=a(x-3)(x+1),
由于抛物线过C(0,-4),
则有:a(0-3)(0+1)=-4,a=
| 4 |
| 3 |
∴抛物线的解析式为y=
| 4 |
| 3 |
| 8 |
| 3 |
(2)假设存在这样的抛物线,其解析式为y=ax2+bx-4.
设△ABC的外接圆圆心为P,连AP、BP,过P作PE⊥x轴于E,PF⊥y轴于F.
 ∵圆P截y轴所得弦长为5,且过点A、B及C(0,-4).
∵圆P截y轴所得弦长为5,且过点A、B及C(0,-4).∴圆P过点D(0,1)
∴P点在x轴下方,
∴CF=DF=
| 5 |
| 2 |
| 5 |
| 2 |
| 3 |
| 2 |
∵∠APE=
| 1 |
| 2 |
∴tan∠APE=
| AE |
| PE |
∴AE=2PE=3,
∴AB=2AE=6,
∵OA•OB=OC•OD,即-x1x2=4.
∴
| 4 |
| a |
∴抛物线的解析式为y=x2+bx-4.
∵AB=6,
∴x1-x2=6.
∴(x1-x2)2=(x1+x2)2-4x1x2=b2+16=36.
∴b=±2
| 5 |
∴存在这样的抛物线y=x2±2
| 5 |
点评:本题主要考查了二次函数解析式的确定,综合考查了一次函数的应用、三角形的外接圆等知识点,综合性强,难度较大.

练习册系列答案
相关题目