题目内容
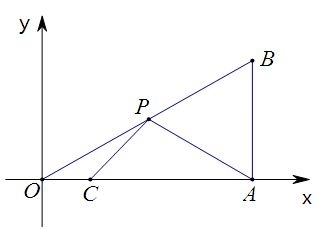
如图,在平面直角坐标系中,Rt△OAB的顶点A的坐标为(9,0),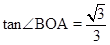 ,点C的坐标为(2,0),点P为斜边OB上的一个动点,则PA+PC的最小值为_______________.
,点C的坐标为(2,0),点P为斜边OB上的一个动点,则PA+PC的最小值为_______________.
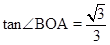 ,点C的坐标为(2,0),点P为斜边OB上的一个动点,则PA+PC的最小值为_______________.
,点C的坐标为(2,0),点P为斜边OB上的一个动点,则PA+PC的最小值为_______________.
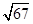 .
.试题分析:作A关于OB的对称点D,连接CD交OB于P,连接AP,过D作DN⊥OA于N,则此时PA+PC的值最小,求出AM,求出AD,求出DN、CN,根据勾股定理求出CD,即可得出答案.
作A关于OB的对称点D,连接CD交OB于P,连接AP,过D作DN⊥OA于N,则此时PA+PC的值最小,
∵Rt△OAB的顶点A的坐标为(9,0),
∴OA=9,
∵tan∠BOA=
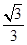 ,
,∴AB=
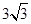 ,∠B=60°,
,∠B=60°,∴∠AOB=30°,
∴OB=2AB=
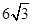 ,
,由三角形面积公式得:S△OAB=
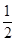 ×OA×AB=
×OA×AB=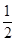 ×OB×AM,即9×
×OB×AM,即9×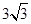 =
=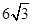 AM,
AM,∴AM=
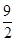 ,
,∴AD=2×
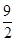 =9,
=9,∵∠AMB=90°,∠B=60°,
∴∠BAM=30°,
∵∠BAO=90°,
∴∠OAM=60°,
∵DN⊥OA,
∴∠NDA=30°,
∴AN=
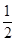 AD=
AD=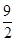 ,由勾股定理得:DN=
,由勾股定理得:DN= ,
,∵C(2,0),
∴CN=9-
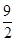 -2=
-2=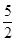 ,
,在Rt△DNC中,由勾股定理得:DC=
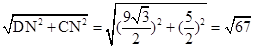
即PA+PC的最小值是
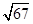 ,
,故答案为:
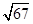 .
.
练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
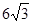 ,AD⊥AC,连接CD.点E在AC上,
,AD⊥AC,连接CD.点E在AC上,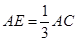 ,过点E作MN⊥AC,分别交AB、CD于点M、N.
,过点E作MN⊥AC,分别交AB、CD于点M、N.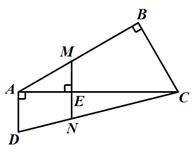
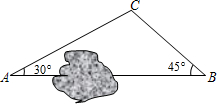
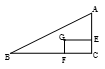
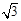 AC,那么∠A= 度.
AC,那么∠A= 度.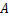 出发,沿北偏东60°方向走了
出发,沿北偏东60°方向走了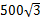 m到达
m到达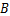 点,然后再沿北偏西
点,然后再沿北偏西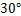 方向走了
方向走了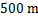 到达目的地
到达目的地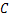 点.求:
点.求: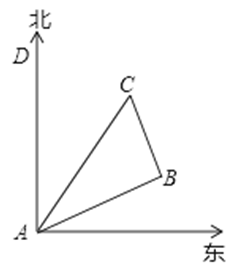
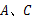 两地之间的距离;
两地之间的距离;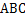 中,
中,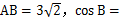
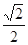 ,
,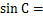
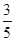 ,则△
,则△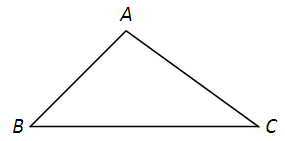
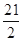
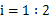 的坡面向上前进了10 m,此时小球距离地面的高度为( )
的坡面向上前进了10 m,此时小球距离地面的高度为( )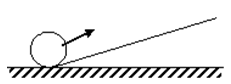
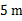
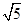 m
m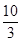 m
m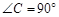 ,∠A、∠B、∠C的对边分别为a、b、c,则下列式子一定成立的是
,∠A、∠B、∠C的对边分别为a、b、c,则下列式子一定成立的是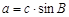 B、
B、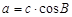
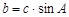 D、
D、