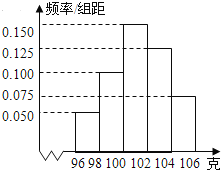
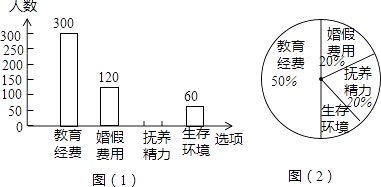
题目内容
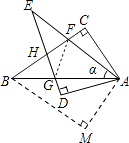
【题目】如图,在四边形ACBM中,∠C=∠M=90°,∠CAB=∠MAB=60°,将△ABM绕点A顺时针旋转α(α<∠BAC),得到Rt△ADE,其中斜边AE交BC于点F,直角边DE分别交AB,BC于点G,H.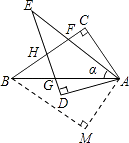
(1)求证:△ACB≌△AMB;
(2)若α=30°,求证:四边形ADHC是正方形;
(3)若∠AFG=70°,求α的值.
【答案】
(1)
证明:△ACB与△AMB中,
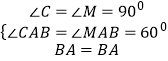 ,
,
∴△ACB≌△AMB(AAS)
(2)
证明:当α=30°时,∠MAD=30°,
∵∠CAB=∠MAB=60°,
∴∠GAD=30°,
∴∠CAD=90°.
∴四边形ADHC是矩形.
∵△ACB≌△AMB,
∴AC=AM=AD,
∴四边形ADHC是正方形
(3)
解:如图,
连接FG,
∵∠CAF+∠FABF=∠GAD+∠FAB,
∴∠CAF=∠GAD,
在△ACF和△ADG中,
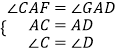 ,
,
∴△ACF≌△ADG(ASA),
∴AF=AG,
∴∠AGF=∠AFG=70°,
∴α=40°.
【解析】(1)根据已知利用全等三角形的判定定理AAS定理可得结论;(2)由旋转可知∠MAD=30°,利用角的加减可得∠GAD=30°,易得∠CAD=90°,又因为∠C=∠D=90°,由矩形的判定定理可知四边形ADHC是矩形,由全等三角形的性质和旋转的性质可得AC=AD,利用正方形的判定定理可得结论;(3)连接FG,利用全等三角形的性质和旋转的性质可得∠CAB=∠DAE,易得∠CAF=∠ADG,易得△ACF≌△ADG,由全等三角形的性质定理可得AF=AG,利用三角形的内角和定理可得结果.

练习册系列答案
相关题目