题目内容
【题目】已知反比例函数y=![]() 的图象与一次函数y=k2x+m的图象交于A(a,1)、B(
的图象与一次函数y=k2x+m的图象交于A(a,1)、B(![]() ,﹣3)两点,连结AO.
,﹣3)两点,连结AO.
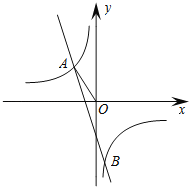
(1)求反比例函数和一次函数的表达式;
(2)根据图象直接写出k2x+m﹣![]() <0的x的取值范围;
<0的x的取值范围;
(3)设点C在y轴上,且与点A、O构成等腰三角形,请直接写出点C的坐标.
【答案】(1)反比例函数关系式为y=﹣![]() ,一次函数关系式为y=﹣3x﹣2;(2)﹣1<x<0或x>
,一次函数关系式为y=﹣3x﹣2;(2)﹣1<x<0或x>![]() ;(3)点C的坐标为:(0,﹣
;(3)点C的坐标为:(0,﹣![]() )或(0,
)或(0,![]() )或(0,2)或(0,1).
)或(0,2)或(0,1).
【解析】
试题分析:(1)将点A(﹣1,a)、B(![]() ,﹣3)代入反比例函数y=
,﹣3)代入反比例函数y=![]() 中得:﹣3×
中得:﹣3×![]() =(﹣1)×a=k1,可求k1、a;再将点A(﹣1,a)、B(
=(﹣1)×a=k1,可求k1、a;再将点A(﹣1,a)、B(![]() ,﹣3)代入y2=k2x+m中,列方程组求k2、m即可;
,﹣3)代入y2=k2x+m中,列方程组求k2、m即可;
(2)根据图象得到一次函数在反比例函数下方时x的取值范围即可求解;
(3)分三种情况:①OA=OC;②AO=AC;③CA=CO;讨论可得点C的坐标.
解:(1)∵反比例函数y=![]() 的图象经过B(
的图象经过B(![]() ,﹣3),
,﹣3),
∴k1=3×![]() ×(﹣3)=﹣3,
×(﹣3)=﹣3,
∵反比例函数y=![]() 的图象经过点A(﹣1,a),
的图象经过点A(﹣1,a),
∴a=1.
由直线y2=k2x+m过点A,B得: ,
,
解得![]() .
.
∴反比例函数关系式为y=﹣![]() ,一次函数关系式为y=﹣3x﹣2;
,一次函数关系式为y=﹣3x﹣2;
(2)k2x+m﹣![]() <0的x的取值范围为﹣1<x<0或x>
<0的x的取值范围为﹣1<x<0或x>![]() ;
;
(3)OA=![]() =
=![]() ,
,
如图,线段OA的垂直平分线与y轴的交点,有1个,点C的坐标为:(0,1);
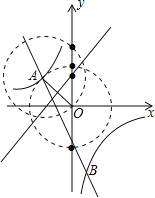
以点A为圆心、AO长为半径的圆与y轴的交点,有1个,点C的坐标为:(0,2);
以点O为圆心、OA长为半径的圆与y轴的交点,有2个,点C的坐标为:(0,﹣![]() )或(0,
)或(0,![]() ).
).
故点C在y轴上,且与点A、O构成等腰三角形,点C的坐标为:(0,﹣![]() )或(0,
)或(0,![]() )或(0,2)或(0,1).
)或(0,2)或(0,1).

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目