��Ŀ����
����Ŀ����ͼ��ijũ���ϰ�������һ��������ȦABCD���������þ�����Ȧ��һ����ȫ����ǽMN��ǽMN�����õij���Ϊ25m�����������ó���Ϊ50m�����Χ�ɣ��������Ҫȫ�����꣬�Ҳ����ǽ�ͷ�IJ��֣�
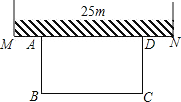
��1����Ҫʹ������Ȧ�����Ϊ300m2����ֱ��ǽ��һ�߳�ABΪ�����ף�
��2��ũ���ϰ����뽫��ȦABCD��������½�������Ϊ320m2���Ӷ��������������������������������������뷨��ʵ����Ϊʲô��
���𰸡���1��15�ף���2�����ܣ����ɼ�����
��������
�����������1������Χ����ABCD�Ŀ�ABΪx�ף����ADΪ��50��2x���ף����ݾ�������ļ��㷽���г�������⣮
��2����ʹ�������Ϊ320����x��ʵ���������Բ���Χ�ɾ��γ��أ�
�⣺��1������Χ����ABCD�Ŀ�ABΪx�ף����ADΪ��50��2x���ף�
�����⣬��x��50��2x��=300��
����x2��25x+150=0��
��˷��̣���x1=15��x2=10��
��ǽ�ij��Ȳ�����25m��
��x2=10�������⣬Ӧ��ȥ��
����ֱ��ǽ��һ�߳�ABΪ15�ף�
��2�����ܣ�
��Ϊ��x��50��2x��=320��x2��25x+160=0��6�֣���
����b2��4ac=��25��2��4��1��160=��15��0��
����������û��ʵ������
��ˣ�����ʹ��Χ���γ��ص����Ϊ320m2��