题目内容
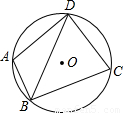
如图,⊙O过四边形ABCD的四个顶点,已知∠ABC=90°,BD平分∠ABC,则:①AD=CD,②
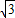 BD=AB+CB,③点O是∠ADC平分线上的点,④AB2+BC2=2CD2,
BD=AB+CB,③点O是∠ADC平分线上的点,④AB2+BC2=2CD2,上述结论中正确的编号是 .
【答案】分析:根据角平分线的定义可得∠ABD=∠CBD=45°,再根据同圆或等圆中,同弧所对的圆周角相等可得 =
= ,然后根据同弧所对的弦相等可得AD=CD,判断出①正确;连接AC,根据直径所对的圆周角是直角可得点O在AC上,根据等腰三角形三线合一的性质可得点O是∠ADC平分线上的点,判断出③正确;再利用勾股定理求出AB2+BC2=2CD2,判断出④正确;点B的位置确定,②
,然后根据同弧所对的弦相等可得AD=CD,判断出①正确;连接AC,根据直径所对的圆周角是直角可得点O在AC上,根据等腰三角形三线合一的性质可得点O是∠ADC平分线上的点,判断出③正确;再利用勾股定理求出AB2+BC2=2CD2,判断出④正确;点B的位置确定,②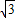 BD=AB+CB无法求出.
BD=AB+CB无法求出.
解答: 解:∵∠ABC=90°,BD平分∠ABC,
解:∵∠ABC=90°,BD平分∠ABC,
∴∠ABD=∠CBD=45°,
∴ =
=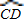 ,
,
∴AD=CD,故①正确;
连接AC,∵∠ABC=90°,
∴点O在AC上,AC为⊙O的直径,
又∵AD=CD,
∴点O是∠ADC平分线上的点,故③正确;
在Rt△ABC中,AB2+BC2=AC2,
在Rt△ACD中,AC2=AD2+CD2=2CD2,
∴AB2+BC2=2CD2,故④正确;
∵点B的位置不确定,
∴ BD=AB+CB无法求出,故②错误;
BD=AB+CB无法求出,故②错误;
综上所述,正确的结论有①③④.
故答案为:①③④.
点评:本题考查了圆周角定理,角平分线的定义,直径所对的圆周角是直角,在同圆或等圆中,同弧所对的圆周角相等,勾股定理的应用,综合题,但难度不大.
 =
= ,然后根据同弧所对的弦相等可得AD=CD,判断出①正确;连接AC,根据直径所对的圆周角是直角可得点O在AC上,根据等腰三角形三线合一的性质可得点O是∠ADC平分线上的点,判断出③正确;再利用勾股定理求出AB2+BC2=2CD2,判断出④正确;点B的位置确定,②
,然后根据同弧所对的弦相等可得AD=CD,判断出①正确;连接AC,根据直径所对的圆周角是直角可得点O在AC上,根据等腰三角形三线合一的性质可得点O是∠ADC平分线上的点,判断出③正确;再利用勾股定理求出AB2+BC2=2CD2,判断出④正确;点B的位置确定,②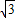 BD=AB+CB无法求出.
BD=AB+CB无法求出.解答:
 解:∵∠ABC=90°,BD平分∠ABC,
解:∵∠ABC=90°,BD平分∠ABC,∴∠ABD=∠CBD=45°,
∴
 =
=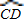 ,
,∴AD=CD,故①正确;
连接AC,∵∠ABC=90°,
∴点O在AC上,AC为⊙O的直径,
又∵AD=CD,
∴点O是∠ADC平分线上的点,故③正确;
在Rt△ABC中,AB2+BC2=AC2,
在Rt△ACD中,AC2=AD2+CD2=2CD2,
∴AB2+BC2=2CD2,故④正确;
∵点B的位置不确定,
∴
 BD=AB+CB无法求出,故②错误;
BD=AB+CB无法求出,故②错误;综上所述,正确的结论有①③④.
故答案为:①③④.
点评:本题考查了圆周角定理,角平分线的定义,直径所对的圆周角是直角,在同圆或等圆中,同弧所对的圆周角相等,勾股定理的应用,综合题,但难度不大.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
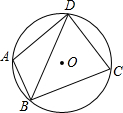 (2013•下城区二模)如图,⊙O过四边形ABCD的四个顶点,已知∠ABC=90°,BD平分∠ABC,则:
(2013•下城区二模)如图,⊙O过四边形ABCD的四个顶点,已知∠ABC=90°,BD平分∠ABC,则: BD=AB+CB,③点O是∠ADC平分线上的点,④
BD=AB+CB,③点O是∠ADC平分线上的点,④ ,上述结论中正确的编号是 .
,上述结论中正确的编号是 .
 BD=AB+CB,③点O是∠ADC平分线上的点,④
BD=AB+CB,③点O是∠ADC平分线上的点,④ ,上述结论中正确的编号是 .
,上述结论中正确的编号是 .
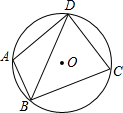 如图,⊙O过四边形ABCD的四个顶点,已知∠ABC=90°,BD平分∠ABC,则:
如图,⊙O过四边形ABCD的四个顶点,已知∠ABC=90°,BD平分∠ABC,则: BD=AB+CB,③点O是∠ADC平分线上的点,④AB2+BC2=2CD2,
BD=AB+CB,③点O是∠ADC平分线上的点,④AB2+BC2=2CD2,