题目内容
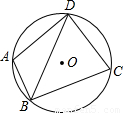
如图,⊙O过四边形ABCD的四个顶点,已知∠ABC=90º,BD平分∠ABC,则:①AD=CD,②  BD=AB+CB,③点O是∠ADC平分线上的点,④
BD=AB+CB,③点O是∠ADC平分线上的点,④ ,上述结论中正确的编号是 .
,上述结论中正确的编号是 .
【答案】
①③④
【解析】
试题分析:①连接AC,因为∠ABC=90º,BD平分∠ABC,所以∠ABD=∠DBC=45°,所以弧AD=弧DC,所以∠DAC=∠DCA,所以AD=CD;② 根据已知条件,只能得出 (即直径),
(即直径),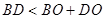 ,得不出
,得不出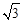 BD=AB+CB,③因为AD=DC,∠ADC=90°,O是AC的中点,根据等腰三角形三线合一,则点O是∠ADC平分线上的点,④在直角三角形ABC中,
BD=AB+CB,③因为AD=DC,∠ADC=90°,O是AC的中点,根据等腰三角形三线合一,则点O是∠ADC平分线上的点,④在直角三角形ABC中,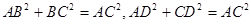 ,因为AD=CD,所以
,因为AD=CD,所以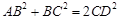 故①③④正确.
故①③④正确.
考点:圆的性质和勾股定理
点评:该题分析较为复杂,所用的知识点比较常用,主要考查学生对圆的基本性质以及对勾股定理的理解和应用。

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
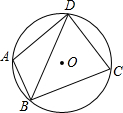 (2013•下城区二模)如图,⊙O过四边形ABCD的四个顶点,已知∠ABC=90°,BD平分∠ABC,则:
(2013•下城区二模)如图,⊙O过四边形ABCD的四个顶点,已知∠ABC=90°,BD平分∠ABC,则: BD=AB+CB,③点O是∠ADC平分线上的点,④
BD=AB+CB,③点O是∠ADC平分线上的点,④ ,上述结论中正确的编号是 .
,上述结论中正确的编号是 .
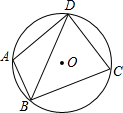 如图,⊙O过四边形ABCD的四个顶点,已知∠ABC=90°,BD平分∠ABC,则:
如图,⊙O过四边形ABCD的四个顶点,已知∠ABC=90°,BD平分∠ABC,则: BD=AB+CB,③点O是∠ADC平分线上的点,④AB2+BC2=2CD2,
BD=AB+CB,③点O是∠ADC平分线上的点,④AB2+BC2=2CD2,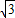 BD=AB+CB,③点O是∠ADC平分线上的点,④AB2+BC2=2CD2,
BD=AB+CB,③点O是∠ADC平分线上的点,④AB2+BC2=2CD2,