题目内容
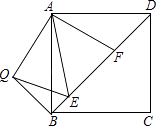
【题目】如图所示，△ABC是直角三角形，∠A=90°，D是斜边BC的中点，E、F分别是AB、AC边上的动点，且DE⊥DF．
（1）如图1，AB=AC，BE=12，CF=5，求线段EF的长．
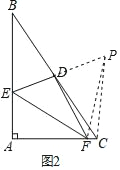
（2）如图2，若AB≠AC，写出线段EF与线段BE、CF之间的等量关系，并写出证明过程．
【答案】（1）13；（2）EF2=BE2+CF2，证明见解析.
【解析】
（1）首先连接AD，由△ABC是等腰直角三角形，AB＝AC，AD是斜边的中线，可得：AD＝DC，∠EAD＝∠C＝45°，AD⊥BC即∠CDF＋∠ADF＝90°，又DE⊥DF，可得：∠EDA＋∠ADF＝90°，故∠EDA＝∠CDF，从而可证：△AED≌△CFD，所以可得：AE＝CF，AF＝BC，即可得出答案；
（2）延长ED到P，使DP＝DE，连接FP，CP，利用SAS得到三角形BED与三角形CPD全等，利用全等三角形对应边相等得到BE＝CP，再利用SAS得到撒尿性EDF和三角形PDF全等，利用全等三角形对应边相等得到EF＝FP，利用等角的余角相等得到∠FCP为直角，在直角三角形FCP中，利用勾股定理列出关系式，等量代换即可得证．
（1）如图1，连接AD，
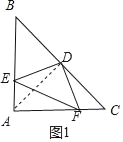
∵在Rt△ABC中，AB=AC，AD为BC边的中线，
∴∠DAC=∠BAD=∠C=45°，AD⊥BC，AD=DC，
又∵DE⊥DF，AD⊥DC，
∴∠EDA+∠ADF=∠CDF+∠FDA=90°，
∴∠EDA=∠CDF
在△AED与△CFD中，
，
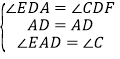∴△AED≌△CFD（ASA）．
∴AE=CF，
同理AF=BE．
∵∠EAF=90°，
∴EF2=DE2+DF2，
∴BE2+CF2=EF2，
∴EF=
=13；
（2）EF2=BE2+CF2；
如图2，延长ED到P，使DP=DE，连接FP，CP，
在△BED和△CPD中，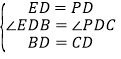 
，
∴△BED≌△CPD（SAS），
∴BE=CP，∠B=∠CPD，
在△EDF和△PDF中，
，
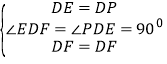∴△EDF≌△PDF（SAS），
∴EF=FP，
∵∠B=∠DCP，∠A=90°，
∴∠B+∠ACB=90°，
∴∠ACB+∠DCP=90°，即∠FCP=90°，
在Rt△FCP中，根据勾股定理得：CF2+CP2=PF2，
∵BE=CP，PF=EF，
∴EF2=BE2+CF2．
