题目内容
【题目】 如图,已知△ABC,AB=AC=1,∠A=36°,∠ABC的平分线BD交AC于点D,则AD的长是 , cosA的值是 . (结果保留根号) 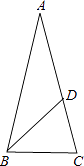
【答案】![]() ;
;![]()
【解析】解:∵△ABC,AB=AC=1,∠A=36°, ∴∠ABC=∠ACB= ![]() =72°.
=72°.
∵BD是∠ABC的平分线,
∴∠ABD=∠DBC= ![]() ∠ABC=36°.
∠ABC=36°.
∴∠A=∠DBC=36°,
又∵∠C=∠C
∴△ABC∽△BDC,
∴ ![]() ,
,
设AD=x,则BD=BC=x.则 ![]() =
= ![]() ,
,
解得:x= ![]() (舍去)或
(舍去)或 ![]() .
.
故x= ![]() .
.
如右图,过点D作DE⊥AB于点E,
∵AD=BD,
∴E为AB中点,即AE= ![]() AB=
AB= ![]() .
.
在Rt△AED中,cosA=  =
= ![]() .
.
故答案是: ![]() ;
; ![]() .
.
【考点精析】掌握黄金分割和相似三角形的判定与性质是解答本题的根本,需要知道把线段AB分成两条线段AC,BC(AC>BC),并且使AC是AB和BC的比例中项,叫做把线段AB黄金分割,点C叫做线段AB的黄金分割点,其中AC=0.618AB;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.

练习册系列答案
相关题目