Question

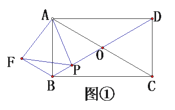
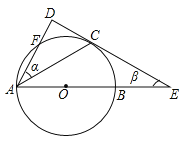
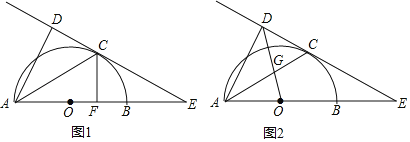
【题目】（新洲区月考）如图1，AB为半圆O的直径，C为圆弧上一点，过点C的直线与AB的延长线交于点E，AD⊥CE于点D，AC平分∠DAB.

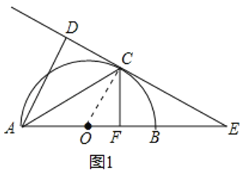
（1）求证：CE是⊙O的切线.

（2）若AB＝6，B为OE的中点，CF⊥AB，垂足为点F，求CF的长；

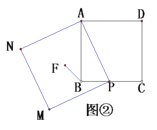
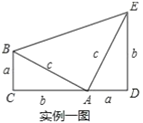
（3）如图2，连接OD交AC于点G，若，求sinE的值.

Answer 1

【答案】（1）详见解析；（2）；（3）

【解析】

（1）连接OC，由AC为角平分线得到一对角相等，再由等边对等角得到一对角相等，等量代换得到一对内错角相等，进而得到OC与AD平行，由AD与CE垂直，得到OC与CE垂直，即可得证；

（2）由OB＝BE，根据半径OA的长求出OE的长，在直角三角形OCE中，根据OCOE得到∠E＝30°，在直角三角形CEF中，利用30°所对的直角边等于斜边的一半即可求出CF的长；

（3）连接OC，由（1）得到OC与AD平行，进而得到三角形OCG与三角形ADG相似，三角形OCE与三角形ADE相似，由相似得比例求出的值，即可确定出sinE的值．

（1）连接OC，

∵AC平分∠DAB，

∴∠DAC＝∠CAO，

∵OA＝OC，

∴∠OAC＝∠ACO，

∵∠DAC＝∠ACO，

∴OC∥AD，

∵AD⊥CE，

∴OC⊥CE，

∴CE为⊙O的切线；

（2）∵AB＝6，OB＝BE，

∴OE＝6，

在Rt△OCE中，

∵OC＝3，OE＝6，

∴∠E＝30°，

∴CE＝3，

∴在Rt△CFE中，CF；

（3）连接OC，

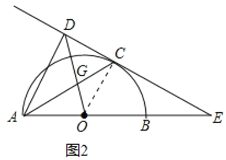
由（1）得OC∥AD，

∴△COG∽△ADG，△COE∽△DAE，

∴，，

∴，

∴，

又∵AO＝CO，

∴，

在Rt△OCE中，sinE．