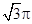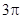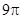题目内容
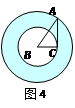
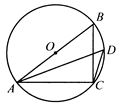
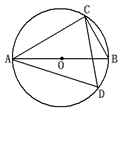
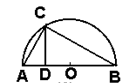
如图，AB是⊙O的直径，C、D是圆上的两点(不与A、B重合)，已知BC＝1，
an∠ADC＝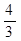
，则AB＝__________．
an∠ADC＝
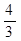，则AB＝__________．
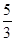
根据同弧所对的圆周角相等得到∠B=∠D，则tanB=tanD=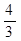，再根据直径所对的圆周角为直角得到∠ACB=90°，然后在Rt△ABC中，利用正切求出AC，再根据勾股定理计算出AB．
解：∵∠B=∠D，
∴tanB=tanD=，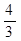
又∵AB为⊙O的直径，
∴∠ACB=90°，
在Rt△ABC中，BC=1，
∴tanB=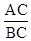
=，
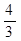∴AC=，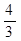
∴AB=
=．
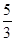故答案为．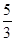
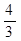，再根据直径所对的圆周角为直角得到∠ACB=90°，然后在Rt△ABC中，利用正切求出AC，再根据勾股定理计算出AB．解：∵∠B=∠D，
∴tanB=tanD=
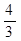，又∵AB为⊙O的直径，
∴∠ACB=90°，
在Rt△ABC中，BC=1，
∴tanB=
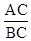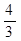=，∴AC=
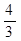，∴AB=
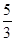=．故答案为
．
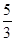练习册系列答案
中考利剑中考试卷汇编系列答案
教育世家状元卷系列答案
相关题目
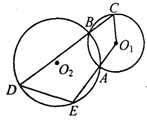
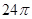
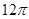
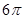
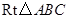中，
，
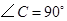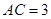．将其绕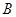
点顺时针旋转一周，则分别以BA，BC为半径的圆形成一圆环．该圆环的面积为 
