题目内容
(本题满分10分)
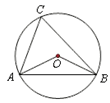
如图等腰三角形ABC中,AB=AC=3,BC=2
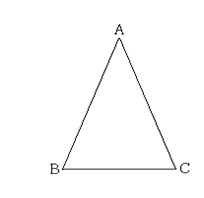
小题1:(1)求作一个圆,使它经过A、B、C三点(保留作图痕迹);
小题2:(2)求所作圆的直径长.
如图等腰三角形ABC中,AB=AC=3,BC=2

小题1:(1)求作一个圆,使它经过A、B、C三点(保留作图痕迹);
小题2:(2)求所作圆的直径长.
小题1:略
小题2:(2)
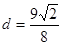
分析:
(1)由于三角形的外心是三角形三边中垂线的交点,可作△ABC的任意两边的垂直平分线,它们的交点即为△ABC的外接圆的圆心(设圆心为O);以O为圆心、OB长为半径作圆,即可得出△ABC的外接圆,即圆O为所求;
(2)设圆的直径为d,半径为r,连接AO并延长交BC于点D,利用等腰三角形的性质和勾股定理先求出圆的半径,则d=2r即可求出此圆的直径。
解答:
解:(1)分别作AB,AC的垂直平分线交点即为圆心,以OB为半径画圆,则圆O为所求;
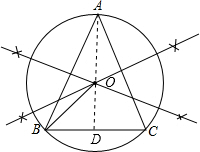
(2)设圆的直径为d,连接AO并延长交BC于点D,
∵△ABC是等腰三角形,
∴AD⊥BC,BD=CD=1/2BC=1,
在Rt△ADB中,AD2=AB 2-BD 2=9-1=8
∴AD=2
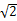 。
。设圆O半径为r,在Rt△BOD中,r2=BD2+OD2,
即:r2=12+(2
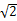 -r)2,
-r)2,解得:r=9
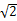 /16,
/16,∴d=9
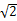 /8。
/8。点评:此题主要考查的是三角形外接圆的作法,关键是画出三角形三边中垂线,找到外接圆的圆心和等腰三角形的性质以及勾股定理的运用。

练习册系列答案
相关题目
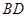 为⊙O的直径,∠A=35°,则
为⊙O的直径,∠A=35°,则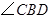 的度数为 。
的度数为 。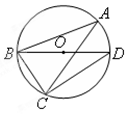
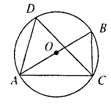
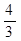 ,则AB=__________.
,则AB=__________.