Ő‚ńŅńŕ»›
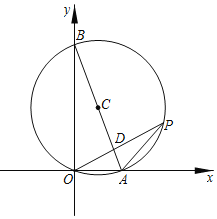
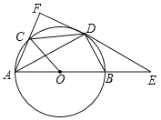
°ĺŐ‚ńŅ°Ņ“—÷™£ļ»ÁÕľ£¨°—OĶńįŽĺ∂ő™r£¨‘ŕ…šŌŖOM…Ō»ő»°“ĽĶ„P£®≤Ľ”ŽĶ„O÷ōļŌ£©£¨»ÁĻŻ…šŌŖOM…ŌĶńĶ„P'£¨¬ķ◊„OP°§OP'=r2£¨‘Ú≥∆Ķ„P'ő™Ķ„PĻō”ŕ°—OĶń∑ī—›Ķ„£ģ

‘ŕ∆Ĺ√ś÷ĪĹ«◊ÝĪÍŌĶxOy÷–£¨“—÷™°—OĶńįŽĺ∂ő™2£ģ
(1)“—÷™Ķ„A (4£¨0)£¨«ůĶ„AĻō”ŕ°—OĶń∑ī—›Ķ„A'Ķń◊ÝĪÍ£Ľ
(2)»ŰĶ„BĻō”ŕ°—OĶń∑ī—›Ķ„B'«°ļ√ő™÷ĪŌŖ![]() ”Ž÷ĪŌŖx=4ĶńĹĽĶ„£¨«ůĶ„BĶń◊ÝĪÍ£Ľ
”Ž÷ĪŌŖx=4ĶńĹĽĶ„£¨«ůĶ„BĶń◊ÝĪÍ£Ľ
(3)»ŰĶ„Cő™÷ĪŌŖ![]() …Ō“Ľ∂ĮĶ„£¨«“Ķ„CĻō”ŕ°—OĶń∑ī—›Ķ„C'‘ŕ°—OĶńńŕ≤Ņ£¨«ůĶ„CĶńļŠ◊ÝĪÍmĶń∑∂őߣĽ
…Ō“Ľ∂ĮĶ„£¨«“Ķ„CĻō”ŕ°—OĶń∑ī—›Ķ„C'‘ŕ°—OĶńńŕ≤Ņ£¨«ůĶ„CĶńļŠ◊ÝĪÍmĶń∑∂őߣĽ
(4)»ŰĶ„Dő™÷ĪŌŖx=4…Ō“Ľ∂ĮĶ„£¨÷ĪĹ”–ī≥ŲĶ„DĻō”ŕ°—OĶń∑ī—›Ķ„D'ĶńļŠ◊ÝĪÍtĶń∑∂őߣģ

°ĺīūįł°Ņ£®1£©A°Į(1£¨0)£Ľ£®2£©B(![]() £¨
£¨![]() )£Ľ£®3£©m >1ĽÚ m <-1£Ľ£®4£©0<t°‹1£ģ
)£Ľ£®3£©m >1ĽÚ m <-1£Ľ£®4£©0<t°‹1£ģ
°ĺĹ‚őŲ°Ņ
£®1£©”…∑ī—›Ķ„Ķń∂®“ŚŅ…«ůĹ‚£Ľ
£®2£©Ō»«ů≥ŲĶ„B'◊ÝĪÍ£¨Ņ…«ůOB'Ķń≥§£¨”…∑ī—›Ķ„Ķń∂®“ŚŅ…«ůOBĶń≥§£¨ľīŅ…«ůĹ‚£Ľ
£®3£©”…Ő‚“‚Ņ…Ķ√OC'£ľ2£¨«“OCOC'=4£¨Ņ…Ķ√OC£ĺ2£¨ľīĶ„C‘ŕ°—OĶńÕ‚≤Ņ£¨ľīŅ…«ůĹ‚£Ľ
£®4£©”…Ő‚“‚Ņ…Ķ√OD°›4£¨«“ODOD'=4£¨Ņ…Ķ√0£ľOD'°‹1£¨ľīŅ…«ůĹ‚£ģ
£®1£©°ŖĶ„A £®4£¨0£©£¨
°ŗOA=4£¨
°ŖĶ„A'ő™Ķ„AĻō”ŕ°—OĶń∑ī—›Ķ„£¨
°ŗOAOA'=22=4£¨
°ŗOA'=1£¨
°ŗA'◊ÝĪÍ£®1£¨0£©£Ľ
£®2£©»ÁÕľ£¨ĻżĶ„B◊ųBE°Õx÷Š”ŕĶ„E£¨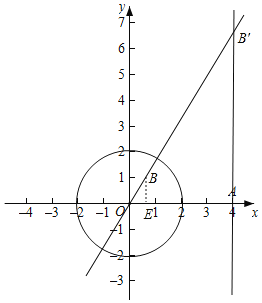
°ŖB'«°ļ√ő™÷ĪŌŖ![]() ”Ž÷ĪŌŖx=4ĶńĹĽĶ„£¨
”Ž÷ĪŌŖx=4ĶńĹĽĶ„£¨
°ŗ![]() £¨
£¨
°ŗ ![]() Ķ„◊ÝĪÍő™(4£¨
Ķ„◊ÝĪÍő™(4£¨![]() )£ģ
)£ģ
°ŗOA=4£¨AB'=![]() £¨
£¨
°ŗ ![]() £¨
£¨
°Ŗ![]() £¨
£¨
![]() £¨
£¨
°ŖĶ„B'ő™Ķ„BĻō”ŕ°—OĶń∑ī—›Ķ„£¨
°ŗOBOB'=22=4£¨
°ŗOB=![]() £¨
£¨
°Ŗ°ŌOBE=90°„-°ŌBOE=30°„£¨
°ŗ![]() £¨
£¨![]() £¨
£¨
°ŗĶ„B◊ÝĪÍő™(![]() £¨
£¨![]() )£Ľ
)£Ľ
£®3£©°ŖĶ„Cő™÷ĪŌŖ![]() …Ō“Ľ∂ĮĶ„£¨«“Ķ„CĻō”ŕ°—OĶń∑ī—›Ķ„C'‘ŕ°—OĶńńŕ≤Ņ£¨
…Ō“Ľ∂ĮĶ„£¨«“Ķ„CĻō”ŕ°—OĶń∑ī—›Ķ„C'‘ŕ°—OĶńńŕ≤Ņ£¨
°ŗ![]() £¨
£¨
°ŖOCOC'=4£¨
°ŗOC![]() £¨
£¨
°ŗĶ„C‘ŕ°—OĶńÕ‚≤Ņ£¨÷ĪŌŖ![]() ”Ž°—OĶńŃĹłŲĹĽĶ„◊ÝĪÍĶńļŠ◊ÝĪÍő™
”Ž°—OĶńŃĹłŲĹĽĶ„◊ÝĪÍĶńļŠ◊ÝĪÍő™![]() £¨
£¨
°ŗ mĶń»°÷Ķ∑∂őß « m >1ĽÚ m <-1£ģ
£®4£©°ŖĶ„Dő™÷ĪŌŖ![]() …Ō“Ľ∂ĮĶ„£¨
…Ō“Ľ∂ĮĶ„£¨
°ŗOD°›4£¨
°ŖODOD'=4£¨
°ŗ0£ľOD'°‹1£¨
°ŗD'ĶńļŠ◊ÝĪÍtĶń∑∂őß «£ļ0£ľt°‹1£ģ

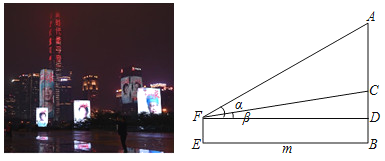
°ĺŐ‚ńŅ°Ņń≥–£ő™Ķų≤ť°įÕ£Ņő≤ĽÕ£—ß°Ī∆ŕľšĺŇńÍľ∂—ß…ķ∆Ĺĺý√ŅŐž…ŌÕÝŅő Ī≥§£¨ňśĽķ≥ť»°Ńň![]() √ŻĺŇńÍľ∂—ß…ķ◊ŲÕݬÁő ĺŪĶų≤ť£ģĻ≤ňńłŲ—°ŌÓ£ļ
√ŻĺŇńÍľ∂—ß…ķ◊ŲÕݬÁő ĺŪĶų≤ť£ģĻ≤ňńłŲ—°ŌÓ£ļ![]() –° Ī“‘Ō¬)°Ę
–° Ī“‘Ō¬)°Ę![]() –° Ī)°Ę
–° Ī)°Ę![]() –° Ī)£¨
–° Ī)£¨ ![]() –° Ī“‘…Ō)£¨√Ņ»ň÷Ľń‹—°“Ľ
–° Ī“‘…Ō)£¨√Ņ»ň÷Ľń‹—°“Ľ
ŌÓ£ģ≤ĘĹęĶų≤ťĹŠĻŻĽś÷∆≥…»ÁŌ¬≤ĽÕÍ’ŻĶńÕ≥ľ∆ĪŪļÕÕ≥ľ∆Õľ£ģ
ĪĽĶų≤ť—ß…ķ∆Ĺĺý√ŅŐž…ŌÕÝŅő ĪľšÕ≥ľ∆ĪŪ
Ī≥§ | ňý’ľįŔ∑÷Ī» |
|
|
|
|
|
|
|
|
ļŌľ∆ |
|
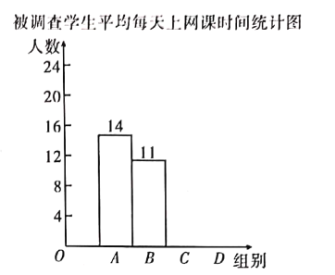
łý囓‘…Ō–ŇŌĘ£¨Ĺ‚īūŌ¬Ń–ő Ő‚£ļ
![]() £¨
£¨![]() £¨
£¨
![]() ≤Ļ»ęŐű–őÕ≥ľ∆Õľ£Ľ
≤Ļ»ęŐű–őÕ≥ľ∆Õľ£Ľ
![]() ł√–£”–ĺŇńÍľ∂—ß…ķ
ł√–£”–ĺŇńÍľ∂—ß…ķ![]() √Ż£¨«Žń„Ļņľ∆Ŕŕ–£ĺŇńÍľ∂—ß…ķ∆Ĺĺý√ŅŐž…ŌÕÝŅő Ī≥§‘ŕ
√Ż£¨«Žń„Ļņľ∆Ŕŕ–£ĺŇńÍľ∂—ß…ķ∆Ĺĺý√ŅŐž…ŌÕÝŅő Ī≥§‘ŕ![]() –° Īľį“‘…ŌĶńĻ≤∂ŗ…Ŕ√Ż£Ľ
–° Īľį“‘…ŌĶńĻ≤∂ŗ…Ŕ√Ż£Ľ
![]() ‘ŕĪĽĶų≤ťĶń∂‘Ōů÷–£¨∆Ĺĺý√ŅŐžĻŘŅī Ī≥§≥¨Ļż
‘ŕĪĽĶų≤ťĶń∂‘Ōů÷–£¨∆Ĺĺý√ŅŐžĻŘŅī Ī≥§≥¨Ļż![]() –° ĪĶń£¨”–
–° ĪĶń£¨”–![]() √Żņī◊‘ĺŇ
√Żņī◊‘ĺŇ![]() įŗ£¨
įŗ£¨![]() √Żņī◊‘ĺŇ
√Żņī◊‘ĺŇ![]() įŗ£¨∆š”ŗ∂ľņī◊‘ĺŇ
įŗ£¨∆š”ŗ∂ľņī◊‘ĺŇ![]() įŗ£¨Ō÷ĹŐĶľī¶◊ľĪłī”
įŗ£¨Ō÷ĹŐĶľī¶◊ľĪłī”![]() —°ŌÓ÷–»ő—°ŃĹ√Ż—ß…ķĹÝ––ĶÁĽį∑√Őł£¨«Ž”√Ń–ĪŪ∑®ĽÚĽ≠ ų◊īÕľĶń∑Ĺ∑®«ůňý≥ť»°Ķń
—°ŌÓ÷–»ő—°ŃĹ√Ż—ß…ķĹÝ––ĶÁĽį∑√Őł£¨«Ž”√Ń–ĪŪ∑®ĽÚĽ≠ ų◊īÕľĶń∑Ĺ∑®«ůňý≥ť»°Ķń![]() √Ż—ß…ķ«°ļ√ņī◊‘Õ¨“ĽłŲįŗľ∂ĶńłŇ¬ £ģ
√Ż—ß…ķ«°ļ√ņī◊‘Õ¨“ĽłŲįŗľ∂ĶńłŇ¬ £ģ