题目内容
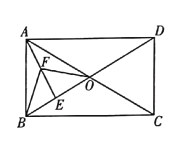
【题目】已知:如图,AB是⊙O的直径,△ABC内接于⊙O.点D在⊙O上,AD平分∠CAB交BC于点E,DF是⊙O的切线,交AC的延长线于点F.
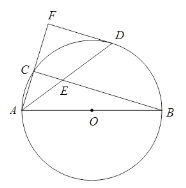
(1)求证;DF⊥AF;
(2)若⊙O的半径是5, AD=8,求DF的长.
【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)连接OD,得OD⊥DF,借助AD平分∠CAB,证明AF∥OD,可证DF⊥AF;
(2)证明△FAD∽△DAB,可得DF长.
(1)证明:连接OD.
∵DF是⊙O的切线,
∴OD⊥DF.
∴∠ODF =90°.
∵AD平分∠CAB,
∴∠CAD =∠DAB.
又∵OA=OD,
∴∠DAB =∠ADO.
∴∠CAD =∠ADO.
∴AF∥OD.
∴∠F+∠ODF =180°.
∴∠F =180°-∠ODF=90°.
∴DF⊥AF.
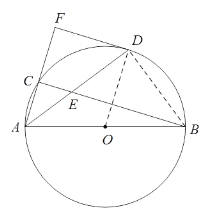
(2)解:连接DB.
∵AB是直径,⊙O的半径是5, AD=8,
∴∠ADB=90°,AB=10.
∴![]() .
.
∵∠F=∠ADB=90°,∠FAD =∠DAB,
∴△FAD∽△DAB.
∴![]() .
.
∴![]() .
.

【题目】某校开设了“3D”打印、数学史、诗歌欣赏、陶艺制作四门校本课程,为了解学生对这四门校本课程的喜爱情况,对学生进行了随机问卷调查(问卷调查表如图所示),将调查结果整理后绘制例图1、图2两幅均不完整的统计图表.
校本课程 | 频数 | 频率 |
A | 36 | 0.45 |
B |
| 0.25 |
C | 16 | b |
D | 8 |
|
合计 | a | 1 |
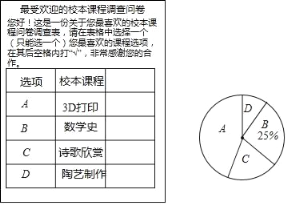
请您根据图表中提供的信息回答下列问题:
(1)统计表中的a= ,b= ;
(2)“D”对应扇形的圆心角为 度;
(3)根据调查结果,请您估计该校2000名学生中最喜欢“数学史”校本课程的人数;
(4)小明和小亮参加校本课程学习,若每人从“A”、“B”、“C”三门校本课程中随机选取一门,请用画树状图或列表格的方法,求两人恰好选中同一门校本课程的概率.
【题目】甲、乙两个药店销售同一种口罩,在甲药店,不论一次购买数量是多少,价格均为3元/个;在乙药店,一次性购买数量不超过100个时,价格为3.5元/个;一次性购买数量超过100个时,其中100个的价格仍为3.5元/个,超过100个的部分的价格为2.5元/个.
(1)根据题意填表:
一次性购买数量(个) | 50 | 100 | 150 |
甲药店花费(元) |
| 300 |
|
乙药店花费(元) |
| 300 |
|
(2)当一次性购买多少个口罩时,在乙药店购买比在甲药店购买可以节约100元?