题目内容
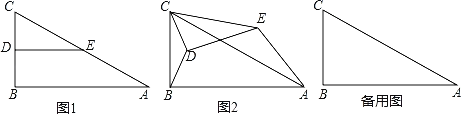
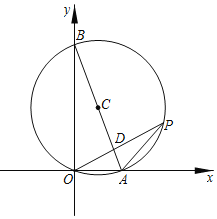
【题目】如图所示，已知A，B两点的坐标分别为（2
，0），（0，10），P是△AOB外接圆⊙C上的一点，OP交AB于点 D．
（1）当OP⊥AB时，求OP；
（2）当∠AOP＝30°时，求AP．
【答案】（1）OP＝
；（2）AP＝2
．
【解析】
（1）当OP⊥AB时，由垂径定理可知OD=DP，根据等面积可求出斜边上的高OD的长，进而可求出PO的长；
（2）连接CP，由圆周角定理可知∠ACP=60°，进而可证明△ACP为等边三角形，则AP=AC，即求出圆的半径即可．
（1）∵A，B两点的坐标分别为（2
，0），（0，10），
∴AO＝2，OB＝10，
∵AO⊥BO，
∴AB＝
＝4，
∵OP⊥AB，
∴
＝
，CD＝DP，
∴CD＝
，
∴OP＝2CD＝；
（2）连接CP，如图所示：
∵∠AOP＝30°，
∴∠ACP＝60°，
∵CP＝CA，
∴△ACP为等边三角形，
∴AP＝AC＝
AB＝2．
练习册系列答案
阅读快车系列答案
相关题目
【题目】某校举行了自贡市创建全国文明城市知识竞赛活动，初一年级全体同学参加了知识竞赛．
收集教据：现随机抽取了初一年级
名同学的“创文知识竞赛”成绩，分数如下（单位：分）：
整理分析数据：
成绩 | 频数（人数） |
|
|
|
|
|
|
|
|
（1）请将图表中空缺的部分补充完整；
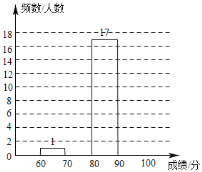
（2）学校决定表彰“创文知识竞赛”成绩在
分及其以上的同学．根据上面统计结果估计该校初一年级
人中，约有多少人将获得表彰；
（3）“创文知识竞赛”中，受到表彰的小红同学得到了印有龚扇、剪纸、彩灯、恐龙图案的四枚纪念章，她从中选取两枚送给弟弟，则小红送给弟弟的两枚纪念章中，恰好有恐龙图案的概率是______________．
