题目内容
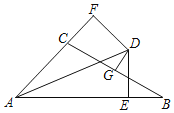
【题目】已知等边△AOB的边长为4,以O为坐标原点,OB所在直线为x轴建立如图所示的平面直角坐标系.
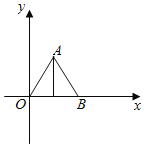
(1)求点A的坐标;
(2)若直线y=kx(k>0)与线段AB有交点,求k的取值范围;
(3)若点C在x轴正半轴上,以线段AC为边在第一象限内作等边△ACD,求直线BD的解析式.
【答案】(1)点A的坐标为(2,2![]() );(2)0<k≤
);(2)0<k≤![]() ;(3)y=
;(3)y=![]() x﹣4
x﹣4![]()
【解析】
(1)如下图所示,过点A作AD⊥x轴于点D,则AD=OAsin∠AOB=4sin60°=2![]() ,同理OA=2,即可求解;
,同理OA=2,即可求解;
(2)若直线y=kx(k>0)与线段AB有交点,当直线过点A时,将点A坐标代入直线的表达式得:2![]() k=2,解得:k=
k=2,解得:k=![]() ,即可求解;
,即可求解;
(3)证明△ACO≌△ADB(SAS),而∠DBC=180°﹣∠ABO﹣∠ABD=180°﹣60°﹣60°=60°,即可求解.
解:(1)如下图所示,过点A作AD⊥x轴于点D,
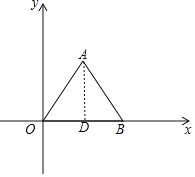
则AD=OAsin∠AOB=4sin60°=![]() ,
,
同理OA=2,
故点A的坐标为(2,2![]() );
);
(2)若直线y=kx(k>0)与线段AB有交点,
当直线过点A时,将点A坐标代入直线的表达式得:2![]() k=2,解得:k=
k=2,解得:k=![]() ,
,
直线OB的表达式为:y=0,而k>0,
故:k的取值范围为:0<k≤![]() ;
;
(3)如下图所示,连接BD,
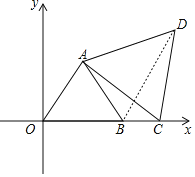
∵△OAB是等边三角形,∴AO=AB,
∵△ADC为等边三角形,∴AD=AC,
∠OAC=∠OAB+∠CAB=60°+∠CAB=∠DAC+∠CAB=∠DAB,
∴△ACO≌△ADB(SAS),
∴∠AOB=∠ABD=60°,
∴∠DBC=180°﹣∠ABO﹣∠ABD=180°﹣60°﹣60°=60°,
故直线BD表达式的k值为tan60°=![]() ,
,
设直线BD的表达式为:y=![]() x+b,
x+b,
将点B(4,0)代入上式得![]()
解得:b=﹣4![]() ,
,
故:直线BD的表达式为:y=![]() x﹣4
x﹣4![]() .
.

 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案