题目内容
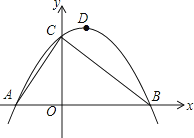
【题目】如图,已知抛物线y=x2+bx与直线y=2x+4交于A(a,8)、B两点,点P是抛物线上A、B之间的一个动点,过点P分别作x轴、y轴的平行线与直线AB交于点C和点E.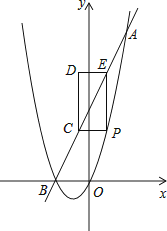
(1)求抛物线的解析式;
(2)若C为AB中点,求PC的长;
(3)如图,以PC,PE为边构造矩形PCDE,设点D的坐标为(m,n),请求出m,n之间的关系式.
【答案】
(1)
解:∵A(a,8)是抛物线和直线的交点,
∴A点在直线上,
∴8=2a+4,解得a=2,
∴A点坐标为(2,8),
又A点在抛物线上,
∴8=22+2b,解得b=2,
∴抛物线解析式为y=x2+2x
(2)
解:联立抛物线和直线解析式可得 ![]() ,解得
,解得 ![]() ,
, ![]() ,
,
∴B点坐标为(﹣2,0),
如图,过A作AQ⊥x轴,交x轴于点Q,
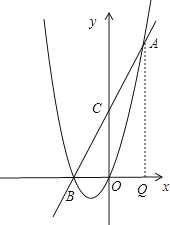
则AQ=8,OQ=OB=2,即O为BQ的中点,
当C为AB中点时,则OC为△ABQ的中位线,即C点在y轴上,
∴OC= ![]() AQ=4,
AQ=4,
∴C点坐标为(0,4),
又PC∥x轴,
∴P点纵坐标为4,
∵P点在抛物线线上,
∴4=x2+2x,解得x=﹣1﹣ ![]() 或x=
或x= ![]() ﹣1,
﹣1,
∵P点在A、B之间的抛物线上,
∴x=﹣1﹣ ![]() 不合题意,舍去,
不合题意,舍去,
∴P点坐标为( ![]() ﹣1,4),
﹣1,4),
∴PC= ![]() ﹣1﹣0=
﹣1﹣0= ![]() ﹣1;
﹣1;
(3)
解:∵D(m,n),且四边形PCDE为矩形,
∴C点横坐标为m,E点纵坐标为n,
∵C、E都在直线y=2x+4上,
∴C(m,2m+4),E( ![]() ,n),
,n),
∵PC∥x轴,
∴P点纵坐标为2m+4,
∵P点在抛物线上,
∴2m+4=x2+2x,整理可得2m+5=(x+1)2,解得x= ![]() ﹣1或x=﹣
﹣1或x=﹣ ![]() ﹣1(舍去),
﹣1(舍去),
∴P点坐标为( ![]() ﹣1,2m+4),
﹣1,2m+4),
∴DE= ![]() ﹣m,CP=
﹣m,CP= ![]() ﹣1﹣m,
﹣1﹣m,
∵四边形PCDE为矩形,
∴DE=CP,即 ![]() ﹣m=
﹣m= ![]() ﹣1﹣m,
﹣1﹣m,
整理可得n2﹣4n﹣8m﹣16=0,
即m、n之间的关系式为n2﹣4n﹣8m﹣16=0
【解析】(1)把A点坐标代入直线方程可求得a的值,再代入抛物线可求得b的值,可求得抛物线解析式;(2)联立抛物线和直线解析式可求得B点坐标,过A作AQ⊥x轴,交x轴于点Q,可知OC= ![]() AQ=4,可求得C点坐标,结合条件可知P点纵坐标,代入抛物线解析式可求得P点坐标,从而可求得PC的长;(3)根据矩形的性质可分别用m、n表示出C、P的坐标,根据DE=CP,可得到m、n的关系式.本题为二次函数的综合应用,涉及知识点有图象的交点、待定系数法、三角形中位线定理、矩形的性质等.在(1)中注意交点坐标的应用,在(2)中求出C点坐标是解题的关键,在(3)中用m、n表示出P点的坐标是解题的关键.本题知识点较多,计算量较大,难度适中.
AQ=4,可求得C点坐标,结合条件可知P点纵坐标,代入抛物线解析式可求得P点坐标,从而可求得PC的长;(3)根据矩形的性质可分别用m、n表示出C、P的坐标,根据DE=CP,可得到m、n的关系式.本题为二次函数的综合应用,涉及知识点有图象的交点、待定系数法、三角形中位线定理、矩形的性质等.在(1)中注意交点坐标的应用,在(2)中求出C点坐标是解题的关键,在(3)中用m、n表示出P点的坐标是解题的关键.本题知识点较多,计算量较大,难度适中.
【考点精析】解答此题的关键在于理解抛物线与坐标轴的交点的相关知识,掌握一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2

【题目】现从A,B两市场向甲、乙两地运送水果,A,B两个水果市场分别有水果35和15吨,其中甲地需要水果20吨,乙地需要水果30吨,从A到甲地运费50元/吨,到乙地30元/吨;从B到甲地运费60元/吨,到乙地45元/吨
(1)设A市场向甲地运送水果x吨,请完成表:
运往甲地(单位:吨) | 运往乙地(单位:吨) | |
A市场 | x |
|
B市场 |
|
|
(2)设总运费为W元,请写出W与x的函数关系式,写明x的取值范围;
(3)怎样调运水果才能使运费最少?运费最少是多少元?