题目内容
正三角形的外接圆半径是R，则它的边长是（ ）
分析：作出正三角形的边心距，连接正三角形的一个顶点和中心可得到一直角三角形，解直角三角形即可．
解答：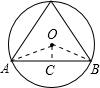
解：如图OA=R，∠AOB=360°÷3=120°
连接OA，OB，作OC⊥AB于点C，
∵OA=OB，
∴AB=2AC，∠AOC=60°，
∴AC=OA×sin60°=
R，
那么正三角形的边长=
R．
故选：B．
解：如图OA=R，∠AOB=360°÷3=120°连接OA，OB，作OC⊥AB于点C，
∵OA=OB，
∴AB=2AC，∠AOC=60°，
∴AC=OA×sin60°=
| ||
| 2 |
那么正三角形的边长=
| 3 |
故选：B．
点评：此题主要考查了三角形的外接圆与外心以及等边三角形的性质，解正多边形和圆的问题时，应连接圆心和正多边形的顶点，作出边心距，得到和中心角一半有关的直角三角形进行求解．
练习册系列答案
相关题目
已知正三角形的外接圆半径为
cm，则它的边长是（ ）
| 2 |
| 3 |
| 3 |
A、
| ||
B、2
| ||
| C、2cm | ||
| D、1cm |
已知正三角形的边长为6，则这个正三角形的外接圆半径是（ ）
A、
| ||
B、2
| ||
| C、3 | ||
D、3
|