题目内容
已知正三角形的边长为6，则这个正三角形的外接圆半径是（ ）
A、
| ||
B、2
| ||
| C、3 | ||
D、3
|
分析：先根据题意画出图形，再根据正三角形的特点求出∠BOC的度数，由等腰三角形的性质及直角三角形的性质解答即可．
解答：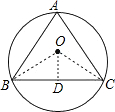
解：如图所示，连接OB，OC，过O作OD⊥BC；
∵△ABC是正三角形，
∴∠BOC=
=120°，
∵OB=OC，∴∠BOD=
=60°，
∴∠OBD=30°，OB=
=
=2
．
故选B．
解：如图所示，连接OB，OC，过O作OD⊥BC；∵△ABC是正三角形，
∴∠BOC=
| 360° |
| 3 |
∵OB=OC，∴∠BOD=
| 120° |
| 2 |
∴∠OBD=30°，OB=
| BD |
| cos30° |
| 3 | ||||
|
| 3 |
故选B．
点评：解决本题的关键是构造与外接圆半径相关的直角三角形．
练习册系列答案
阅读快车系列答案
相关题目
已知正三角形的边长为6，则其内切圆的半径为（ ）
A、2
| ||
| B、3 | ||
C、
| ||
| D、1 |
已知正三角形的边长为3，则它的外接圆的面积为（ ）
| A、3π | ||||
| B、6π | ||||
| C、9π | ||||
D、
|
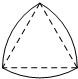如图，“凸轮”的外围由以正三角形的顶点为圆心，以正三角形的边长为半径的三段等弧组成．已知正三角形的边长为1，则凸轮的周长等于（ ）