题目内容
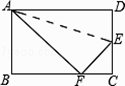
【题目】如图,把矩形纸片ABCD置于直角坐标系中,AB∥x轴,BC∥y轴,AB=4,BC=3,点B(5,1)翻折矩形纸片使点A落在对角线DB上的H处得折痕DG.
(1)求AG的长;
(2)在坐标平面内存在点M(m,﹣1)使AM+CM最小,求出这个最小值;
(3)求线段GH所在直线的解析式.
【答案】
(1)
解:由折叠的性质可得,AG=GH,AD=DH,GH⊥BD,
∵AB=4,BC=3,
∴BD= ![]() =5,
=5,
设AG的长度为x,
∴BG=4﹣x,HB=5﹣3=2,
在Rt△BHG中,GH2+HB2=BG2,
x2+4=(4﹣x)2,
解得:x=1.5,
即AG的长度为1.5
(2)
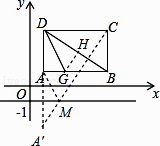
解:如图所示:作点A关于直线y=﹣1的对称点A',连接CA'与y=﹣1交于M点,
∵点B(5,1),
∴A(1,1),C(5,4),A'(1,﹣3),
AM+CM=A'C= ![]() =
= ![]() ,
,
即AM+CM的最小值为 ![]()
(3)
解:∵点A(1,1),
∴G(2.5,1),
过点H作HE⊥AD于点E,HF⊥AB于点F,如图所示,
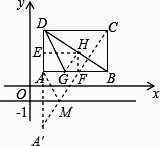
∴△AEH∽△DAB,△HFB∽△DAB,
∴ ![]() =
= ![]() ,
, ![]() =
= ![]() ,
,
即 ![]() =
= ![]() ,
, ![]() =
= ![]() ,
,
解得:EH= ![]() ,HF=
,HF= ![]() ,
,
则点H( ![]() ,
, ![]() ),
),
设GH所在直线的解析式为y=kx+b,
则  ,
,
解得: 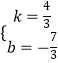 ,
,
则解析式为:y= ![]() x﹣
x﹣ ![]() .
.
【解析】(1)根据折叠的性质可得AG=GH,设AG的长度为x,在Rt△HGB中,利用勾股定理求出x的值;(2)作点A关于直线y=﹣1的对称点A',连接CA'与y=﹣1交于一点,这个就是所求的点,求出此时AM+CM的值;(3)求出G、H的坐标,然后设出解析式,代入求解即可得出解析式.

练习册系列答案
相关题目