��Ŀ����
����Ŀ���ı���ABCD�������Σ���ʾ���������ı���ȣ��ĸ��Ƕ���90����

��1����ͼ1����G��BC��������һ�㣨�����B��C�غϣ�������AG����BF��AG�ڵ�F��DE��AG�ڵ�E��
��֤����ABF�ա�DAE��
��2��ֱ��д����1���У��߶�EF��AF��BF�ĵ�����ϵ�� ����
��3������ͼ2������G��CD��������һ�㣨�����C��D�غϣ�������AG����BF��AG�ڵ�F��DE��AG�ڵ�E����ͼ��ȫ������������ �����߶�EF��AF��BF�ĵ�����ϵ���� ����
����ͼ3������G��CD�ӳ���������һ�㣬����AG����BF��AG�ڵ�F��DE��AG�ڵ�E���߶�EF��AF��BF�ĵ�����ϵ���� ����
��4������G��BC�ӳ���������һ�㣬����AG����BF��AG�ڵ�F��DE��AG�ڵ�E���뻭ͼ��̽���߶�EF��AF��BF�ĵ�����ϵ��
���𰸡���1��֤������������2��EF=AF-BF����3���١�ABF�ա�DAE��EF=BF-AF����EF=AF+BF����2��EF=BF-AF��
�������������������1���������������ʵó�AB��AD����DAB��90�������ݴ�ֱ����ó���AED����AFB��90�������ݵȽǵ������������ADE����BAF������AAS֤����������ȫ�ȼ��ɣ�
��2������ȫ�ȵó�AE��BF�����뼴������𰸣�
��3���١�ABF�ա�DAE��EF��BF��AF��֤���루1����2�����ƣ���EF��AF��BF��֤���������ƣ�
��4���������������ʵó�AB��AD����DAB��90�������ݴ�ֱ����ó���AED����AFB��90���������ADE����BAF������AAS֤����������ȫ�ȼ��ɣ�
���������
��1��֤�������ı���ABCD�������Σ�
��AB��AD����DAB��90����
���DAE����BAE��90����
��DE��AG��BF��AG��
���AED����AFB��90����
���EAD����ADE��90����
���ADE����BAF��
������ABF����DAE��
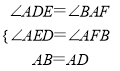 ��
��
���ABF�ա�DAE��AAS����
��2���⣺�߶�EF��AF��BF�ĵ�����ϵ��EF��AF��BF��
�����ǣ����ɣ�1��֪����ABF�ա�DAE��
��BF��AE��
��EF��AF��AE��AF��BF��
�ʴ�Ϊ��EF��AF��BF��
��3���ٽ⣺��ABF�ա�DAE��EF��BF��AF��
�����ǣ����ı���ABCD�������Σ�
��AB��AD����DAB��90����
���DAE����BAE��90����
��DE��AG��BF��AG��
���AED����AFB��90����
���EAD����ADE��90����
���ADE����BAF��
������ABF����DAE��
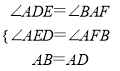
���ABF�ա�DAE��AAS����
��AE��BF��
��EF��AE��AF��BF��AF��
�ʴ�Ϊ����ABF�ա�DAE��EF��BF��AF��
�ڽ⣺EF��AF��BF��
�����ǣ����ı���ABCD�������Σ�
��AB��AD����DAB��90����
���DAE����BAF��180����90����90����
��DE��AG��BF��AG��
���AED����AFB��90����
���EAD����ADE��90����
���ADE����BAF��
������ABF����DAE��
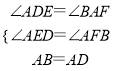 ��
��
���ABF�ա�DAE��AAS����
��AE��BF��
��EF��AE��AF��AF��BF��
�ʴ�Ϊ��EF��AF��BF��
��4���⣺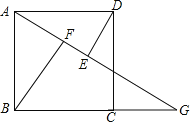
������֤�����ƣ���ABF�ա�DAE��AAS����
��AE��BF��
��EF��AE��AF��BF��AF��
��EF��BF��AF��

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�

