题目内容
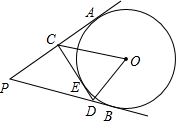 如图,PA、PB是⊙O的切线,CD切⊙O于点E,△PCD的周长为12,∠APB=60°.求:
如图,PA、PB是⊙O的切线,CD切⊙O于点E,△PCD的周长为12,∠APB=60°.求:(1)PA的长;
(2)∠COD的度数.
分析:(1)可通过切线长定理将相等的线段进行转换,得出三角形PDE的周长等于PA+PB的结论,即可求出PA的长;
(2)根据三角形的内角和求出∠ADC和∠BEC的度数和,然后根据切线长定理,得出∠EDO和∠DEO的度数和,再根据三角形的内角和求出∠DOE的度数.
(2)根据三角形的内角和求出∠ADC和∠BEC的度数和,然后根据切线长定理,得出∠EDO和∠DEO的度数和,再根据三角形的内角和求出∠DOE的度数.
解答:解:(1)∵CA,CE都是圆O的切线,
∴CA=CE,
同理DE=DB,PA=PB,
∴三角形PDE的周长=PD+CD+PC=PD+PC+CA+BD=PA+PB=2PA=12,
即PA的长为6;
(2)∵∠P=60°,
∴∠PCE+∠PDE=120°,
∴∠ACD+∠CDB=360°-120°=240°,
∵CA,CE是圆O的切线,
∴∠OCE=∠OCA=
∠ACD;
同理:∠ODE=
∠CDB,
∴∠OCE+∠ODE=
(∠ACD+∠CDB)=120°,
∴∠COD=180-120°=60°.
∴CA=CE,
同理DE=DB,PA=PB,
∴三角形PDE的周长=PD+CD+PC=PD+PC+CA+BD=PA+PB=2PA=12,
即PA的长为6;
(2)∵∠P=60°,
∴∠PCE+∠PDE=120°,
∴∠ACD+∠CDB=360°-120°=240°,
∵CA,CE是圆O的切线,
∴∠OCE=∠OCA=
| 1 |
| 2 |
同理:∠ODE=
| 1 |
| 2 |
∴∠OCE+∠ODE=
| 1 |
| 2 |
∴∠COD=180-120°=60°.
点评:本题考查的是切线长定理,切线长定理图提供了很多等线段,分析图形时关键是要仔细探索,找出图形的各对相等切线长.

练习册系列答案
相关题目
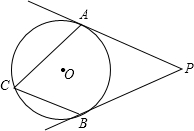 如图,PA,PB是⊙O的切线,切点分别为A,B,且∠APB=50°,点C是优弧
如图,PA,PB是⊙O的切线,切点分别为A,B,且∠APB=50°,点C是优弧
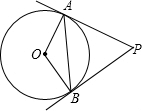 如图,PA、PB是⊙O的切线,A、B为切点,∠OAB=30度.
如图,PA、PB是⊙O的切线,A、B为切点,∠OAB=30度. 4、如图,PA、PB是⊙O的两条切线,A、B是切点,连接AB,直线PO交AB于M.请你根据圆的对称性,写出△PAB的三个正确的结论.
4、如图,PA、PB是⊙O的两条切线,A、B是切点,连接AB,直线PO交AB于M.请你根据圆的对称性,写出△PAB的三个正确的结论.
 (2012•谷城县模拟)如图,PA、PB是⊙O 的切线,切点分别是A、B,点C是⊙O上异与点A、B的点,如果∠P=60°,那么∠ACB等于
(2012•谷城县模拟)如图,PA、PB是⊙O 的切线,切点分别是A、B,点C是⊙O上异与点A、B的点,如果∠P=60°,那么∠ACB等于