题目内容
 如图所示,AB是⊙O的弦,AB的长为24cm,点P是弦AB上一动点,且到圆心的最短距离为5cm,则OP的长的范围是
如图所示,AB是⊙O的弦,AB的长为24cm,点P是弦AB上一动点,且到圆心的最短距离为5cm,则OP的长的范围是5cm≤OP≤13cm
5cm≤OP≤13cm
.分析:过O作OP⊥AB于P,此时OP=5,根据勾股定理求出OB,即可得出答案.
解答: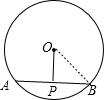
解:过O作OP⊥AB于P,此时OP=5,
由垂径定理得:BP=AP=
AB=12cm
在Rt△OPB中,OP=5cm,OB=12cm,由勾股定理得:OB=
=13(cm),
即P和B或A重和时,OP=13cm,
即OP的范围是5cm≤OP≤13cm.
故答案为:5cm≤OP≤13cm.

解:过O作OP⊥AB于P,此时OP=5,
由垂径定理得:BP=AP=
| 1 |
| 2 |
在Rt△OPB中,OP=5cm,OB=12cm,由勾股定理得:OB=
| 122+52 |
即P和B或A重和时,OP=13cm,
即OP的范围是5cm≤OP≤13cm.
故答案为:5cm≤OP≤13cm.
点评:本题考查了垂径定理和勾股定理的应用,关键是求出O到AB的最短距离和OB的长.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案
相关题目
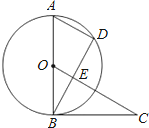 如图所示,AB是⊙O的直径,AD是弦,∠DBC=∠A.
如图所示,AB是⊙O的直径,AD是弦,∠DBC=∠A.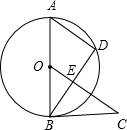 如图所示,AB是⊙O的直径,AD是弦,∠DBC=∠A,OC⊥BD于点E.
如图所示,AB是⊙O的直径,AD是弦,∠DBC=∠A,OC⊥BD于点E.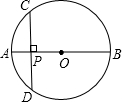 如图所示,AB是⊙O的直径,弦CD⊥AB于点P,CD=10cm,AP:PB=1:5,则⊙O的半径为
如图所示,AB是⊙O的直径,弦CD⊥AB于点P,CD=10cm,AP:PB=1:5,则⊙O的半径为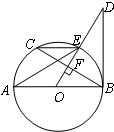 如图所示,AB是⊙O直径,OD⊥弦BC于点F,且交⊙O于点E,且∠AEC=∠ODB.
如图所示,AB是⊙O直径,OD⊥弦BC于点F,且交⊙O于点E,且∠AEC=∠ODB. 如图所示,AB是⊙O直径,∠D=35°,则∠BOC等于( )
如图所示,AB是⊙O直径,∠D=35°,则∠BOC等于( )