ЬтФПФкШн
ЁОЬтФПЁПШчЭМЃЌЖўДЮКЏЪ§y=Љx2+bx+cЕФЭМЯѓгыxжсНЛгкЕуA(Љ1ЃЌ0)ЃЌB(2ЃЌ0)ЃЌгыyжсЯрНЛгкЕуCЃЎ
ЃЈ1ЃЉЧѓЖўДЮКЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉШєЕуEЪЧЕквЛЯѓЯоЕФХзЮяЯпЩЯЕФвЛИіЖЏЕуЃЌЕБЫФБпаЮABECЕФУцЛ§зюДѓЪБЃЌЧѓЕуEЕФзјБъЃЌВЂЧѓГіЫФБпаЮABECЕФзюДѓУцЛ§ЃЛ
ЃЈ3ЃЉШєЕуMдкХзЮяЯпЩЯЃЌЧвдкyжсЕФгвВрЃЎЁбMгыyжсЯрЧаЃЌЧаЕуЮЊDЃЎвдCЃЌDЃЌMЮЊЖЅЕуЕФШ§НЧаЮгыЁїAOCЯрЫЦЃЌЧыжБНгаДГіЕуMЕФзјБъЃЎ
ЁОД№АИЁПЃЈ1ЃЉЖўДЮКЏЪ§ЕФНтЮіЪНЮЊy=Љx2+x+2ЃЛЃЈ2ЃЉЕуEЕФзјБъЮЊ(1ЃЌ2)ЃЌЧвЫФБпаЮABECЕФзюДѓУцЛ§ЮЊ4ЃЛЃЈ3ЃЉЕуMЕФзјБъЮЊ(![]() ЃЌ
ЃЌ ![]() )ЃЌ(
)ЃЌ(![]() ЃЌ
ЃЌ ![]() )ЃЌ(3ЃЌЃ4) .
)ЃЌ(3ЃЌЃ4) .
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉАбAЁЂBЕФзјБъДњШыМДПЩЕУЕНД№АИЃЛ
ЃЈ2ЃЉЩш EЃЈaЃЌbЃЉЃЌЯШБэЪОГіЫФБпаЮABECЕФУцЛ§SЃЌдйХфЗНМДПЩЃЛ
ЃЈ3ЃЉЗжСНжжЧщПіЬжТлЃЌ ![]() ЃЌЛђ
ЃЌЛђ![]() ЃЎ
ЃЎ
ЪдЬтНтЮіЃКЃЈ1ЃЉЁп ЖўДЮКЏЪ§![]() ЕФЭМЯѓгыxжсЯрНЛгкЕуAЃЈЉ1ЃЌ0ЃЉЃЌBЃЈ2ЃЌ0ЃЉЃЌ
ЕФЭМЯѓгыxжсЯрНЛгкЕуAЃЈЉ1ЃЌ0ЃЉЃЌBЃЈ2ЃЌ0ЃЉЃЌ
Ёр![]() ЃЌНтЕУЃК
ЃЌНтЕУЃК ![]() ЃЌЁр ЖўДЮКЏЪ§ЕФНтЮіЪНЮЊ
ЃЌЁр ЖўДЮКЏЪ§ЕФНтЮіЪНЮЊ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШчЭМ1ЃЎ
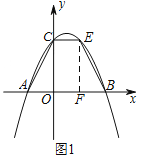
ЁпЖўДЮКЏЪ§ЕФНтЮіЪНЮЊ![]() гыyжсЯрНЛгкЕуCЃЌЁр CЃЈ0ЃЌ2ЃЉЃЌЩш EЃЈaЃЌbЃЉЃЌЧвa >0ЃЌb >0ЃЌЁп AЃЈ-1ЃЌ0ЃЉЃЌBЃЈ2ЃЌ0ЃЉЃЌЁр OA=1ЃЌOB=2ЃЌOC=2ЃЌдђSЫФБпаЮABEC=
гыyжсЯрНЛгкЕуCЃЌЁр CЃЈ0ЃЌ2ЃЉЃЌЩш EЃЈaЃЌbЃЉЃЌЧвa >0ЃЌb >0ЃЌЁп AЃЈ-1ЃЌ0ЃЉЃЌBЃЈ2ЃЌ0ЃЉЃЌЁр OA=1ЃЌOB=2ЃЌOC=2ЃЌдђSЫФБпаЮABEC= ![]() =
= ![]() ЃЌЁп Еу EЃЈaЃЌbЃЉЪЧЕквЛЯѓЯоЕФХзЮяЯпЩЯЕФвЛИіЖЏЕуЃЌЁр
ЃЌЁп Еу EЃЈaЃЌbЃЉЪЧЕквЛЯѓЯоЕФХзЮяЯпЩЯЕФвЛИіЖЏЕуЃЌЁр![]() ЃЌЁр
ЃЌЁр![]() ЃЌЁр ЕБЫФБпаЮABECЕФУцЛ§зюДѓЪБЃЌЕуEЕФзјБъЮЊЃЈ1ЃЌ4ЃЉЃЌЧвЫФБпаЮABECЕФзюДѓУцЛ§ЮЊ4ЃЛ
ЃЌЁр ЕБЫФБпаЮABECЕФУцЛ§зюДѓЪБЃЌЕуEЕФзјБъЮЊЃЈ1ЃЌ4ЃЉЃЌЧвЫФБпаЮABECЕФзюДѓУцЛ§ЮЊ4ЃЛ
ЃЈ3ЃЉШчЭМ2ЃЎ
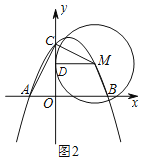
ЩшMЃЈmЃЌnЃЉЃЌЧвm>0ЃЌЁп ЕуMдкЖўДЮКЏЪ§ЕФЭМЯѓЩЯЃЌЁр![]() ЃЌЁп ЁбMгыyжсЯрЧаЃЌЧаЕуЮЊDЃЌЁр ЁЯMDC =90ЁуЃЌЁп вдCЃЌDЃЌMЮЊЖЅЕуЕФШ§НЧаЮгыЁїAOCЯрЫЦЃЌЁр
ЃЌЁп ЁбMгыyжсЯрЧаЃЌЧаЕуЮЊDЃЌЁр ЁЯMDC =90ЁуЃЌЁп вдCЃЌDЃЌMЮЊЖЅЕуЕФШ§НЧаЮгыЁїAOCЯрЫЦЃЌЁр![]() ЃЌЛђ
ЃЌЛђ![]() ЃЌ
ЃЌ
ЂйЕБn >2ЪБЃЌ ![]() ЃЌНтЕУ m1=0ЃЈЩсШЅЃЉЃЌm2=
ЃЌНтЕУ m1=0ЃЈЩсШЅЃЉЃЌm2=![]() ЃЌ Лђm3=0ЃЈЩсШЅЃЉЃЌm4=-1ЃЈЩсШЅЃЉЃЛ
ЃЌ Лђm3=0ЃЈЩсШЅЃЉЃЌm4=-1ЃЈЩсШЅЃЉЃЛ
ЂкЭЌРэПЩЕУЃЌЕБn<2ЪБЃЌm1=0ЃЈЩсШЅЃЉ ЃЌm2=![]() ЃЌЛђm3=0ЃЈЩсШЅЃЉЃЌm4=3ЃЛ
ЃЌЛђm3=0ЃЈЩсШЅЃЉЃЌm4=3ЃЛ
злЩЯЃЌТњзуЬѕМўЕФЕуMЕФзјБъЮЊЃЈ![]() ЃЌ
ЃЌ ![]() ЃЉЃЌЃЈ
ЃЉЃЌЃЈ![]() ЃЌ
ЃЌ ![]() ЃЉЃЌЃЈ3ЃЌ-4ЃЉЃЎ
ЃЉЃЌЃЈ3ЃЌ-4ЃЉЃЎ






