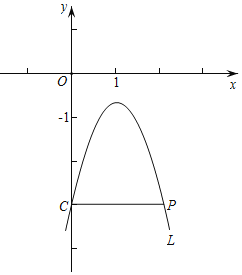题目内容
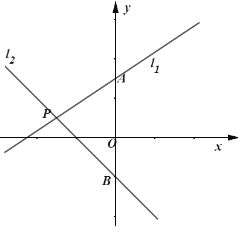
【题目】如图,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() :
:![]() 交
交![]() 轴于点
轴于点![]() ,交直线
,交直线![]() 点
点![]() .
.
(1)求直线![]() 的函数解析式;
的函数解析式;
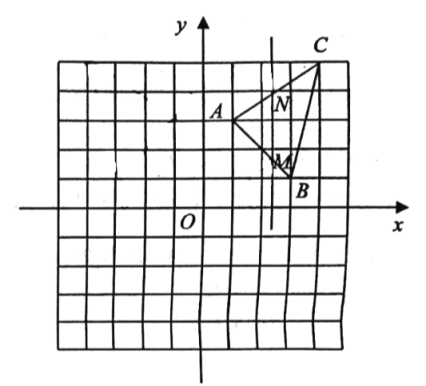
(2)过动点![]() 作
作![]() 轴的垂线与直线
轴的垂线与直线![]() 、
、![]() 分别交于
分别交于![]() 、
、![]() 两点,且
两点,且![]() .
.
①求![]() 的取值范围;
的取值范围;
②若![]() ,直接写出
,直接写出![]() 的值.
的值.
【答案】(1)![]() ;(2)①
;(2)①![]() 且
且![]() ;②
;② ![]() 或
或![]()
【解析】
(1)利用![]() 求出
求出![]() 点坐标为
点坐标为![]() ,再设直线
,再设直线![]() 的函数解析式为y=kx+b,将点A、P的坐标代入解答;
的函数解析式为y=kx+b,将点A、P的坐标代入解答;
(2)①由已知可得:![]() 、
、![]() 两点的坐标分别为:
两点的坐标分别为:![]() ,
,![]() ,分两种情况:当点
,分两种情况:当点![]() 在点
在点![]() 右侧时,点
右侧时,点![]() 在点
在点![]() 的上方,求出
的上方,求出![]() 解得
解得![]() ,当点
,当点![]() 在点
在点![]() 左侧时,点
左侧时,点![]() 在点
在点![]() 的下方,求得
的下方,求得![]() 解得
解得![]() ,由此动点a的取值范围;
,由此动点a的取值范围;
②设![]() ,连接AN1,作N1D⊥y轴于D,PC⊥y轴于C,根据
,连接AN1,作N1D⊥y轴于D,PC⊥y轴于C,根据![]() ,求出OD=1+3=4,由此得到点N1的横坐标是-6,即a=-6;设
,求出OD=1+3=4,由此得到点N1的横坐标是-6,即a=-6;设![]() ,,连接AN2,作N2D⊥y轴于D,PC⊥y轴于C,根据
,,连接AN2,作N2D⊥y轴于D,PC⊥y轴于C,根据![]() ,求出CD=
,求出CD=![]() CB=1,得到点N2的纵坐标是0,由此解得x=-2,得到a=-2.
CB=1,得到点N2的纵坐标是0,由此解得x=-2,得到a=-2.
(1)将点P的坐标代入![]() 中,得t=3-2=1,
中,得t=3-2=1,
∴![]() 点坐标为
点坐标为![]() ,
,
设直线![]() 的函数解析式为y=kx+b,将点A、P的坐标代入,得
的函数解析式为y=kx+b,将点A、P的坐标代入,得
![]() ,解得
,解得![]() ,
,
∴直线![]() 的函数解析式为
的函数解析式为![]() ;
;
(2)①由已知可得:![]() 、
、![]() 两点的坐标分别为:
两点的坐标分别为:![]() ,
,![]() ,
,
当点![]() 在点
在点![]() 右侧时,点
右侧时,点![]() 在点
在点![]() 的上方,
的上方,
∴![]() 解得
解得![]() ,
,
当点![]() 在点
在点![]() 左侧时,点
左侧时,点![]() 在点
在点![]() 的下方,
的下方,
∴![]() 解得
解得![]() ,
,
综上![]() 的取值范围是:
的取值范围是:![]() 且
且![]() (注:没有
(注:没有![]() 不扣分);
不扣分);
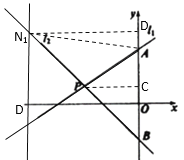
②设![]() ,连接AN1,作N1D⊥y轴于D,PC⊥y轴于C,
,连接AN1,作N1D⊥y轴于D,PC⊥y轴于C,
∵![]() ,
,
∴N1P=PB,
∵B(0,-2),
∴CD=CB=1-(-2)=3,
∴OD=1+3=4,
将y=4代入y=-x-2中得-x-2=4,
解得x=-6,
∴点N1的横坐标是-6,即a=-6;
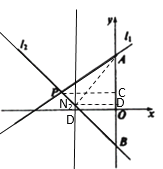
设![]() ,连接AN2,作N2D⊥y轴于D,PC⊥y轴于C,
,连接AN2,作N2D⊥y轴于D,PC⊥y轴于C,
∵![]() ,
,
∴PN2=![]() PB,
PB,
∴CD=![]() CB=1,
CB=1,
∴点N2的纵坐标是0,
将y=0代入y=-x-2中,得x=-2,
∴a=-2,
综上,![]() 或
或![]() .
.

 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案【题目】学校开展“书香校园”活动以来,受到同学们的广泛关注,学校为了解全校学生课外阅读的情况,随机调查了部分学生在一周内借阅图书的次数,并制成如图不完整的统计表
学生借阅图书的次数
借阅图书的次数 | 0次 | 1次 | 2次 | 3次 | 4次及以上 |
人数 | 7 | 13 | a | 10 | 3 |
学生借阅图书的次数统计表

请你根据统计图表的信息,解答下列问题:
(1)a= ;b=
(2)该调查统计数据的中位数是__________次
(3)扇形统计图中,“3次”所对应的扇形圆心角度数是______________;
(4)若该校共有2000名学生,根据调查结果,估计该校学生在一周内借阅图书“4次以上”的人数