题目内容
【题目】如图,已知在Rt△ABC中,∠B=30°,∠ACB=90°,延长CA到O,使AO=AC,以O为圆心,OA长为半径作⊙O交BA延长线于点D,连接CD.
(1)求证:CD是⊙O的切线;
(2)若AB=4,求图中阴影部分的面积.
【答案】(1)证明:连接OD,
∵∠BCA=90°,∠B=30°,
∴∠OAD=∠BAC=60°,
∵OD=OA,
∴△OAD是等边三角形,
∴AD=OA=AC,∠ODA=∠O=60°,
∴∠ADC=∠ACD=![]() ∠OAD=30°,
∠OAD=30°,
∴∠ODC=60°+30°=90°,
即OD⊥DC,
∵OD为半径,
∴CD是⊙O的切线;
(2)解:∵AB=4,∠ACB=90°,∠B=30°,
∴OD=OA=AC=![]() AB=2,
AB=2,
由勾股定理得:CD=![]() =
=![]() =2
=2![]() ,
,
∴S阴影=S△ODC﹣S扇形AOD=![]() ×2×2
×2×2![]() ﹣
﹣![]() =2
=2![]() ﹣
﹣![]() π.
π.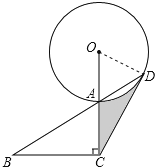
【解析】(1)连接OD,求出∠OAD=60°,得出等边三角形OAD,求出AD=OA=AC,∠ODA=∠O=60°,求出∠ADC=∠ACD=![]() ∠OAD=30°,求出∠ODC=90°,根据切线的判定得出即可;
∠OAD=30°,求出∠ODC=90°,根据切线的判定得出即可;
(2)求出OD,根据勾股定理求出CD长,分别求出三角形ODC和扇形AOD的面积,相减即可.

练习册系列答案
 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
【题目】2013年5月23日起,我市将对行人闯红灯分三档进行处罚,九年级数学研究学习小组在某十字路口随机调查部分市民对该法归的了解情况,统计结果后绘制了如图的三副不完整的统计图,请结合图中相关数据回答下列问题.
得分 | |
A | 50<n≤60 |
B | 60<n≤70 |
C | 70<n≤80 |
D | 80<n≤90 |
E | 90<n≤100 |
(1)本次共调查的人数为;
(2)补全频数分布图; 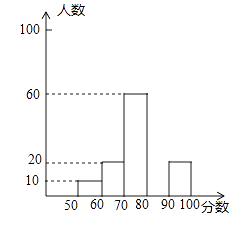
(3)在扇形统计图中,“B”所在的扇形的圆心角的度数为; 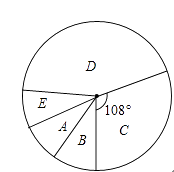
(4)若在这一周里,该路口共有2000人通过,则可估计得分在80以上的人数大约为 .