题目内容
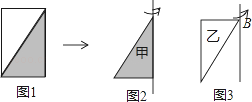
【题目】如图所示,在等边![]() 中,点
中,点![]() 分别在边
分别在边![]() 上.且
上.且![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() .
.
![]() 求
求![]() 的度数;
的度数;
![]() 若
若![]() ,求
,求![]() 的长.
的长.
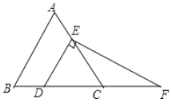
【答案】(1)∠F=30°;(2)DF=8
【解析】
(1)根据等边三角形的性质可得∠ACB=∠B=60°,然后根据平行线的性质可得∠EDC=∠B=60°,再根据三角形的内角和定理即可求出结论;
(2)根据等边三角形的判定定理证出△EDC为等边三角形,从而得出CD=CE=4,然后根据三角形外角的性质即可证出∠CEF=∠F,再根据等角对等边可得CF=CE=4,即可得出结论.
解:(1)∵△ABC是等边三角形
∴∠ACB=∠B=60°
∵![]()
∴∠EDC=∠B=60°
∵![]()
∴∠DEF=90°
∴∠F=180°-∠DEF-∠EDC=30°
(2)∵∠ACB=∠EDC=60°
∴∠DEC=180°-∠ACB-∠EDC=60°
∴△EDC为等边三角形
∴CD=CE=4
∵∠F=30°
∴∠CEF=∠ACB-∠F=30°
∴∠CEF=∠F
∴CF=CE=4
∴DF=CF+CD=8

练习册系列答案
相关题目