题目内容
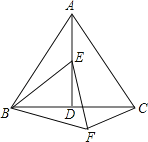
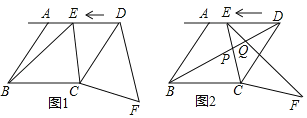
【题目】如图1,在菱形ABCD中,AB=![]() ,tan∠ABC=2,点E从点D出发,以每秒1个单位长度的速度沿着射线DA的方向匀速运动,设运动时间为t(秒),将线段CE绕点C顺时针旋转一个角α(α=∠BCD),得到对应线段CF.
,tan∠ABC=2,点E从点D出发,以每秒1个单位长度的速度沿着射线DA的方向匀速运动,设运动时间为t(秒),将线段CE绕点C顺时针旋转一个角α(α=∠BCD),得到对应线段CF.
(1)求证:BE=DF;
(2)当t= 秒时,DF的长度有最小值,最小值等于 ;
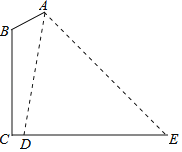
(3)如图2,连接BD、EF、BD交EC、EF于点P、Q,当t为何值时,△EPQ是直角三角形?
【答案】(1)见解析;(2)t=(6![]() +6),最小值等于12;(3)t=6秒或6
+6),最小值等于12;(3)t=6秒或6![]() 秒时,△EPQ是直角三角形
秒时,△EPQ是直角三角形
【解析】
(1)由∠ECF=∠BCD得∠DCF=∠BCE,结合DC=BC、CE=CF证△DCF≌△BCE即可得;
(2)作BE′⊥DA交DA的延长线于E′.当点E运动至点E′时,由DF=BE′知此时DF最小,求得BE′、AE′即可得答案;
(3)①∠EQP=90°时,由∠ECF=∠BCD、BC=DC、EC=FC得∠BCP=∠EQP=90°,根据AB=CD=6![]() ,tan∠ABC=tan∠ADC=2即可求得DE;
,tan∠ABC=tan∠ADC=2即可求得DE;
②∠EPQ=90°时,由菱形ABCD的对角线AC⊥BD知EC与AC重合,可得DE=6![]() .
.
(1)∵∠ECF=∠BCD,即∠BCE+∠DCE=∠DCF+∠DCE,
∴∠DCF=∠BCE,
∵四边形ABCD是菱形,
∴DC=BC,
在△DCF和△BCE中,
 ,
,
∴△DCF≌△BCE(SAS),
∴DF=BE;
(2)如图1,作BE′⊥DA交DA的延长线于E′.
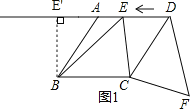
当点E运动至点E′时,DF=BE′,此时DF最小,
在Rt△ABE′中,AB=6![]() ,tan∠ABC=tan∠BAE′=2,
,tan∠ABC=tan∠BAE′=2,
∴设AE′=x,则BE′=2x,
∴AB=![]() x=6
x=6![]() ,x=6,
,x=6,
则AE′=6
∴DE′=6![]() +6,DF=BE′=12,
+6,DF=BE′=12,
时间t=6![]() +6,
+6,
故答案为:6![]() +6,12;
+6,12;
(3)∵CE=CF,
∴∠CEQ<90°,
①当∠EQP=90°时,如图2①,
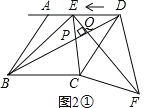
∵∠ECF=∠BCD,BC=DC,EC=FC,
∴∠CBD=∠CEF,
∵∠BPC=∠EPQ,
∴∠BCP=∠EQP=90°,
∵AB=CD=6![]() ,tan∠ABC=tan∠ADC=2,
,tan∠ABC=tan∠ADC=2,
∴DE=6,
∴t=6秒;
②当∠EPQ=90°时,如图2②,
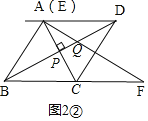
∵菱形ABCD的对角线AC⊥BD,
∴EC与AC重合,
∴DE=6![]() ,
,
∴t=6![]() 秒,
秒,
综上所述,t=6秒或6![]() 秒时,△EPQ是直角三角形.
秒时,△EPQ是直角三角形.

 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案