题目内容
【题目】已知直线![]() 与x轴和y轴分别交于点A和点B,抛物线
与x轴和y轴分别交于点A和点B,抛物线![]() 的顶点M在直线AB上,且抛物线与直线AB的另一个交点为N.
的顶点M在直线AB上,且抛物线与直线AB的另一个交点为N.
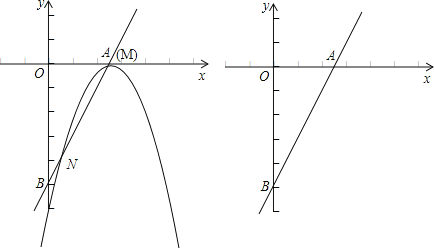
(1)如图,当点M与点A重合时,求:
①抛物线的解析式;
②点N的坐标和线段MN的长;
(2)抛物线![]() 在直线AB上平移,是否存在点M,使得△OMN与△AOB相似?若存在,直接写出点M的坐标;若不存在,请说明理由.
在直线AB上平移,是否存在点M,使得△OMN与△AOB相似?若存在,直接写出点M的坐标;若不存在,请说明理由.
【答案】(1)①![]() ②N(
②N(![]() ,-4),
,-4),![]() (2)存在.点M的坐标为(2,-1)或(4,3)
(2)存在.点M的坐标为(2,-1)或(4,3)
【解析】
(1)①由直线![]() 与x轴和y轴分别交于点A和点B,求出点A、B的坐标,由顶点M与点A重合,根据二次函数的性质求出顶点解析式.
与x轴和y轴分别交于点A和点B,求出点A、B的坐标,由顶点M与点A重合,根据二次函数的性质求出顶点解析式.
②联立![]() 和
和![]() ,求出点N的坐标,过N作NC⊥x轴,由勾股定理求出线段MN的长.
,求出点N的坐标,过N作NC⊥x轴,由勾股定理求出线段MN的长.
(2)根据相似三角形的性质,可得关于m或n的方程,可得M点的坐标,要分类讨论,以防遗漏.
解:(1)①∵直线![]() 与x轴和y轴分别交于点A和点B,
与x轴和y轴分别交于点A和点B,
∴A(![]() ,0),B(0,-5).
,0),B(0,-5).
当顶点M与点A重合时,∴M(![]() ,0).
,0).
∴抛物线的解析式是:![]() ,即
,即![]() .
.
②∵N是直线![]() 与在抛物线
与在抛物线![]() 的交点,
的交点,
∴ ,解得
,解得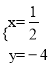 或
或![]() .
.
∴N(![]() ,-4).
,-4).
如图,过N作NC⊥x轴,垂足为C.
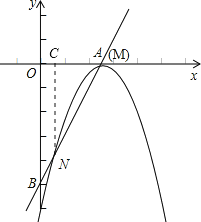
∵N(![]() ,-4),∴C(
,-4),∴C(![]() ,0)
,0)
∴NC=4.MC=OM-OC=![]() .
.
∴![]() .
.
(2)设M(m,2m-5),N(n,2n-5).![]() ,
,
![]() ,
,
则OB=2OA,![]() ,
,
当∠MON=90°时,
∵AB≠MN,且MN和AB边上的高相等,因此△OMN与△AOB不能全等,
∴△OMN与△AOB不相似,不满足题意.
当∠OMN=90°时,![]() ,即
,即![]() ,解得
,解得![]() ,
,
则m2+(2m-5)2=(![]() )2,解得m=2,
)2,解得m=2,
∴M(2,-1);
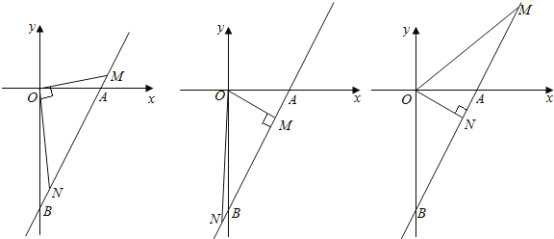
当∠ONM=90°时,![]() ,即
,即![]() ,解得
,解得![]() ,
,
则n2+(2n-5)2=(![]() )2,解得n=2,
)2,解得n=2,
解得:m=4,
则M的坐标是M(4,3).
故M的坐标是:(2,-1)或(4,3).

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目