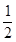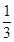题目内容
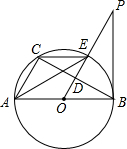
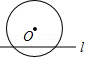
如图，在以O为圆心的两个同心圆中，大圆的弦AB与小圆相切于点C，若AB的长为8cm，则图中阴影部分的面积为 ▲ cm2．
16π。
设AB于小圆切于点C，连接OC，OB。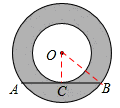
∵AB于小圆切于点C，∴OC⊥AB。
∴BC=AC=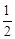
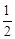AB=×8=4。
∵Rt△OBC中，OB2=OC2+BC2，即OB2－OC2= BC2=16，
∴圆环（阴影）的面积=π•OB2－π•OC2=π（OB2－OC2）=16π（cm2）。
∵AB于小圆切于点C，∴OC⊥AB。
∴BC=AC=
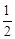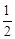AB=×8=4。∵Rt△OBC中，OB2=OC2+BC2，即OB2－OC2= BC2=16，
∴圆环（阴影）的面积=π•OB2－π•OC2=π（OB2－OC2）=16π（cm2）。
练习册系列答案
学而优衔接教材南京大学出版社系列答案
小学课堂作业系列答案
金博士一点全通系列答案
相关题目
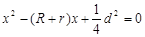有两个相等的实数根，其中R 、r分别是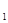⊙O
⊙O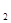
的半径，d为两圆的圆心距，则⊙O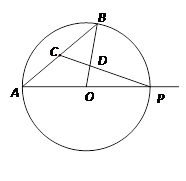
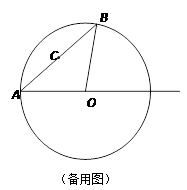
，求y与x的函数关系式并写出自变量x 的取值范围。
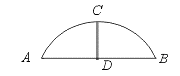
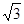米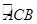
的三等分点，请你判断四边形AOEC为哪种特殊四边形？并说明理由．
