题目内容
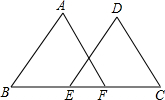已知：如图，E、F两点在BC上，BE=CF，AB∥DE，AF∥CD（1）求证：△ABF≌△DEC；
（2）已知中的图是否为轴对称图形？
答：
否
否
（填：“是”或“否”）分析：（1）根据平行线的性质得到∠B=∠DEC，∠AFB=∠C，由BE=CF得到BF=CE，然后根据“ASA”可判断△ABF≌△DEC；
（2）根据轴对称图形的定义进行判断．
（2）根据轴对称图形的定义进行判断．
解答：（1）证明：∵AB∥DE，AF∥CD
∴∠B=∠DEC，∠AFB=∠C，
∵BE=CF，
∴BF=CE，
在△ABF和△DEC中
，
∴△ABF≌△DEC（ASA）；
（2）解：题中的图不是轴对称图形．
∴∠B=∠DEC，∠AFB=∠C，
∵BE=CF，
∴BF=CE，
在△ABF和△DEC中
|
∴△ABF≌△DEC（ASA）；
（2）解：题中的图不是轴对称图形．
点评：题考查了全等三角形的判定：判定三角形的方法有“SSS”、“ASA”、“SAS”、“AAS”．也考查了轴对称图形．
练习册系列答案
开心练习课课练与单元检测系列答案
开心试卷期末冲刺100分系列答案
相关题目
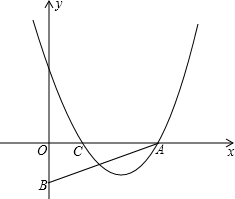C=OB，抛物线y=（x-2）（x-m）-（p-2）（p-m）（m、p为常数且m+2≥2p＞0）经过A、C两点．
（15届江苏初二1试）已知：如图，长方形ABCD被两条线段分割成四个小长方形，如果其中图形Ⅰ、Ⅱ、Ⅲ的面积依次为8、6、5，则阴影部分的面积为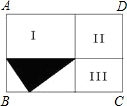
已知：如图，长方形ABCD被两条线段分割成四个小长方形，如果其中图形Ⅰ、Ⅱ、Ⅲ的面积依次为4、3、2，则阴影部分的面积为
已知，如图，A，B两村之间有三条道路，甲，乙两人分别从A，B两村同时出发，他们途中相遇的概率为
已知：如图，锐角△ABC的两条高CD、BE相交于点O，且OB=OC．