题目内容
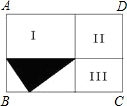已知：如图，长方形ABCD被两条线段分割成四个小长方形，如果其中图形Ⅰ、Ⅱ、Ⅲ的面积依次为4、3、2，则阴影部分的面积为分析：先设Ⅰ、Ⅱ、Ⅲ的长、宽分别是a、b、c、d，根据长方形的面积公式，可得ab=4①，bc=3②，cd=2③，
②③联合可求b=
d④，把④代入①，可求ad，从而可求阴影的面积．
②③联合可求b=
| 3 |
| 2 |
解答：解：如右图所示，设Ⅰ、Ⅱ、Ⅲ的长、宽分别是a、b、c、d，根据题意得
ab=4①，bc=3②，cd=2③，
②÷③得
=
，
∴b=
d④，
把④代入①，得
ad=
，
∴S阴影=
ad=
×
=
．
故答案是
．
ab=4①，bc=3②，cd=2③，
②÷③得
| b |
| d |
| 3 |
| 2 |
∴b=
| 3 |
| 2 |
把④代入①，得
ad=
| 8 |
| 3 |
∴S阴影=
| 1 |
| 2 |
| 1 |
| 2 |
| 8 |
| 3 |
| 4 |
| 3 |
故答案是
| 4 |
| 3 |
点评：本题考查了三角形、长方形面积公式．注意式子之间的变形，通过设未知数可简化计算．
练习册系列答案
相关题目
（15届江苏初二1试）已知：如图，长方形ABCD被两条线段分割成四个小长方形，如果其中图形Ⅰ、Ⅱ、Ⅲ的面积依次为8、6、5，则阴影部分的面积为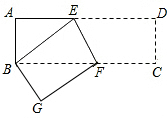
已知，如图，长方形ABCD中，AB=3cm，AD=9cm，将此长方形折叠，使点B与点D重合，折痕为EF，则AE=
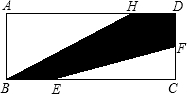已知：如图，长方形ABCD中，F是CD的中点，BC=3BE，AD=4HD．若长方形的面积是300平方米，则阴影部分的面积等于