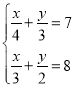题目内容
【题目】（问题背景）
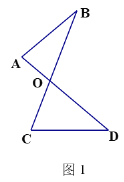
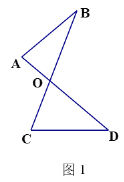
（1）如图1的图形我们把它称为“8字形”，请说理证明∠A+∠B＝∠C+∠D
（简单应用）
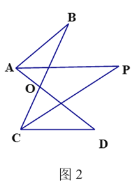
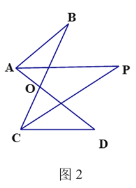
（2）如图2，AP、CP分别平分∠BAD、∠BCD，若∠ABC＝28°，∠ADC＝20°，求∠P的度数（可直接使用问题（1）中的结论）
（问题探究）
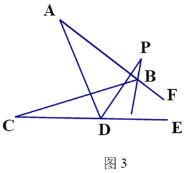
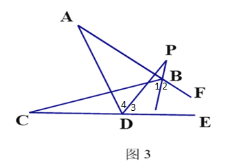
（3）如图3，直线BP平分∠ABC的外角∠FBC，DP平分∠ADC的外角∠ADE，若∠A＝30°，∠C＝18°，则∠P的度数为
（拓展延伸）
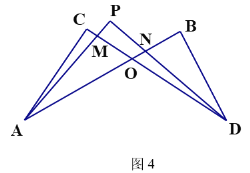
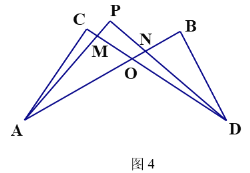
（4）在图4中，若设∠C＝x，∠B＝y，∠CAP＝
∠CAB，∠CDP＝∠CDB，试问∠P与∠C、∠B之间的数量关系为 （用x、y表示∠P）
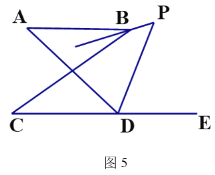
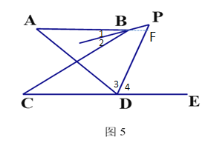
（5）在图5中，BP平分∠ABC，DP平分∠ADC的外角∠ADE，猜想∠P与∠A、∠C的关系，直接写出结论 ．
【答案】（1）证明见解析；（2）24°；（3）24°；（4）∠P=
x+
y；（5）∠P=
【解析】
（1）根据三角形内角和为180°，对顶角相等，即可证得∠A+∠B=∠C+∠D
（2）由（1）的结论得：∠BCP+∠P=∠BAP+∠ABC①，∠PAD+∠P=∠PCD+∠ADC②，将两个式子相加，已知AP、CP分别平分∠BAD、∠BCD，可得∠BAP=∠PAD，∠BCP=∠PCD，可证得∠P=
(∠ABC+∠ADC)，即可求出∠P度数．
（3）已知直线BP平分∠ABC的外角∠FBC，DP平分∠ADC的外角∠ADE，可得∠1=∠2，∠3=∠4，由（1）的结论得：∠C+180°-∠3=∠P+180°-∠1，∠A+∠4=∠P+∠2，两式相加即可求出∠P的度数．
（4）由（1）的结论得：∠CAB+∠C=∠P+∠CDB，∠CAB+∠P=∠B+∠CDB，第一个式子乘以3，得到的式子减去第二个式子即可得出用x、y表示∠P
（5）延长AB交DP于点F，标注出∠1，∠2，∠3，∠4，由（1）的结论得：∠A+2∠1=∠C+180°-2∠3，其中根据对顶角相等，三角形内角和，以及外角的性质即可得到∠1=∠PBF=180°-∠BFP-∠P=180°-(∠A+∠3)-∠P，代入∠A+2∠1=∠C+180°-2∠3，即可得出∠P与∠A、∠C的关系．
（1）如图1，
∠A+∠B+∠AOB=∠C+∠D+∠COD=180°
∵∠AOB=∠COD
∴∠A+∠B=∠C+∠D
（2）∵AP、CP分别平分∠BAD、∠BCD
∴∠BAP=∠PAD，∠BCP=∠PCD，
由（1）的结论得：∠BCP+∠P=∠BAP+∠ABC①，∠PAD+∠P=∠PCD+∠ADC②
①+②，得2∠P+∠PAD+∠BCP=∠BAP+∠ABC +∠PCD+∠ADC
∴∠P=(∠ABC+∠ADC)
∴∠ABC＝28°，∠ADC＝20°
∴∠P=(28°+20°)
∴∠P=24°
故答案为：24°
（3）∵如图3，直线BP平分∠ABC的外角∠FBC，DP平分∠ADC的外角∠ADE，
∴∠1=∠2，∠3=∠4
由（1）的结论得：∠C+180°-∠3=∠P+180°-∠1①，∠A+∠4=∠P+∠2②
①+②，得∠C+180°-∠3+∠A+∠4=∠P+180°-∠1+∠P+∠2
∴30°+18°=2∠P
∴∠P=24°
故答案为：24°
（4）由（1）的结论得：∠CAB+∠C=∠P+∠CDB①，∠CAB+∠P=∠B+∠CDB②
①×3，得∠CAB+3∠C=3∠P+∠CDB③
②-③，得∠P-3x=y-3∠P
∴∠P=x+y
故答案为：∠P=x+y
（5）如图5所示，延长AB交DP于点F
由（1）的结论得：∠A+2∠1=∠C+180°-2∠3
∵∠1=∠PBF=180°-∠BFP-∠P=180°-(∠A+∠3)-∠P
∴∠A+360°-2∠A-2∠3-2∠P=∠C+180°-2∠3
解得：∠P=
故答案为：∠P=
