题目内容
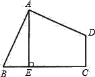
【题目】如图，在△ABC中，AB=AC，AD⊥BC于D点，E、F分别为DB、DC的中点，则图中共有全等三角形 对．
【答案】4．
【解析】试题分析：本题重点是根据已知条件“AB=AC，AD⊥BC交D点，E、F分别是DB、DC的中点”，得出△ABD≌△ACD，然后再由结论推出AB=AC，BE=DE，CF=DF，从而根据“SSS”或“SAS”找到更多的全等三角形，要由易到难，不重不漏．
解：∵AD⊥BC，AB=AC
∴D是BC中点
∴BD=DC，
∵AD=AD，
∴△ABD≌△ACD（SSS）；
E、F分别是DB、DC的中点
∴BE=ED=DF=FC
∵AD⊥BC，AD=AD，ED=DF
∴△ADF≌△ADE（HL）；
∵∠B=∠C，BE=FC，AB=AC
∴△ABE≌△ACF（SAS）
∵EC=BF，AB=AC，AE=AF
∴△ABF≌△ACE（SSS）．
∴全等三角形共4对，分别是：△ABD≌△ACD（HL），△ABE≌△ACF（SAS），△ADF≌△ADE（SSS），△ABF≌△ACE（SAS）．
故答案为4．
练习册系列答案
备战中考寒假系列答案
相关题目
