题目内容
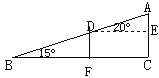
【题目】如图，一勘测人员从B点出发，沿坡角为15°的坡面以5千米/时的速度行至D处，用了12分钟，然后沿坡角为20°的坡面以3千米/时的速度到达山顶A点处，用了10分钟，求山高（即AC的长度）及（即BC的长）（精确到0.01千米）．
【答案】1.44千米
【解析】
试题过D作DF⊥BC于F，先求得BD、AD的长，再在Rt△BFD中，根据正弦函数求得DF、BF的长，在Rt△ADE中，根据余弦函数求得DE、AE的长，即可求得结果.
过D作DF⊥BC于F
由已知得BD=5×
=1(千米)，AD=3×
=0.5(千米)
在Rt△BFD中，DF=BD·sin15°≈0.2588(千米)
BF=BD·cos15°≈0.9659(千米)
在Rt△ADE中，DE=AD·cos20°≈0.4698(千米)
AE=AD·sin20°≈0.1710(千米)
故AC=AE+EC=AE+DF=0.1710+0.2588=0.4298≈0.43(千米)
BC=BF+CF=BF+DE=0.9659+0.4698=1.4357≈1.44(千米).
练习册系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
