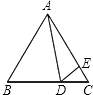题目内容
【题目】以下四种沿AB折叠的方法中,不一定能判定纸带两条边线a,b互相平行的是( )
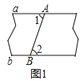


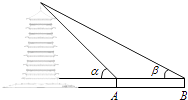
A. 如图1,展开后测得∠1=∠2
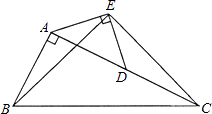
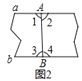
B. 如图2,展开后测得∠1=∠2且∠3=∠4
C. 如图3,测得∠1=∠2
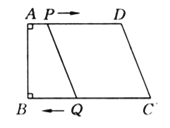
D. 如图4,展开后再沿CD折叠,两条折痕的交点为O,测得OA=OB,OC=OD
【答案】C
【解析】分析:对于选项A,∠1=∠2,而其是一组内错角,根据“内错角相等,两直线平行”判断即可;
对于选项B,根据已知条件可知∠1=∠2=∠3=∠4=90°,根据“内错角相等,两直线平行”或“同旁内角互补,两直线平行”判断即可;
对于选项C,∠1=∠2,其既不是同位角,也不是内错角,结合两直线平行的判定定理即可判断;
对于选项D,首先根据“SAS”得到△AOC≌△BOD,然后根据全等三角形的性质得到∠OAC=∠OBD,最后根据“内错角相等,两直线平行”判断即可.
详解:对于A,因为∠1=∠2,且∠1与∠2是一组内错角,所以a∥b;
对于B,因为∠1=∠2,∠3=∠4,所以∠1=∠2=∠3=∠4=90°,故a∥b;
对于C,根据∠1=∠2无法证得a∥b;
对于D,因为OA=OB,OC=OD,∠AOC=∠BOD,所以△AOC≌△BOD,∠OAC=∠OBD,故a∥b.
故选C.

练习册系列答案
相关题目