题目内容
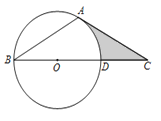
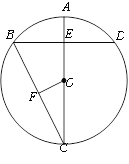
【题目】如图,AC是⊙O的直径,弦BD⊥AO于E,连接BC,过点O作OF⊥BC于F,若BD=16cm,AE=4cm.
(1)求⊙O的半径;
(2)求OF的长.
【答案】(1)10;(2)OF=2![]()
【解析】
(1)连接OB,设半径为R, 则OE=R-4,再由垂径定理求得BE,根据勾股定理求出R即可;(2)根据勾股定理求得BC,证明△CFO∽△CEB,根据相似三角形的性质列出比例式,计算即可

解:(1)连结OB,设半径为R, 则OE=R-4
∵AC是⊙O的直径,弦BD⊥AC于E
∴ BE=DE=8
在Rt△BOE中 , OE2+BE2=OB2
∴ (R-4)2+82=R2
解得R=10.
(2) 根据勾股定理得 BC=8![]()
可证△COF∽△CBE
得![]() =
= ![]() 即
即![]() =
= ![]()
∴ OF=2![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】盒中有若干枚黑棋和白棋,这些棋除颜色外无其他差别,现让学生进行摸棋试验:每次摸出一枚棋,记录颜色后放回摇匀.重复进行这样的试验得到以下数据:
摸棋的次数n | 100 | 200 | 300 | 500 | 800 | 1000 |
摸到黑棋的次数m | 24 | 51 | 76 | 124 | 201 | 250 |
摸到黑棋的频率 | 0.240 | 0.255 | 0.253 | 0.248 | 0.251 | 0.250 |
(1)根据表中数据估计从盒中摸出一枚棋是黑棋的概率是 ;(精确到0.01)
(2)若盒中黑棋与白棋共有4枚,某同学一次摸出两枚棋,请计算这两枚棋颜色不同的概率,并说明理由