题目内容
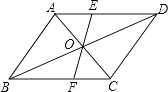
【题目】如图所示,将△ABC沿直线BC方向平移△DEF的位置,G是DE上一点,连接AG,过点A、D作直线MN. 
(1)求证:∠AGE=∠GAD+∠ABC;
(2)若EDF=∠DAG,∠CAG+∠CEG=180°,判断AG与DE的位置关系,并证明你的结论.
【答案】
(1)解:由平移的性质得:△ABC≌△DEF,
∴AB=DE,AB∥DE,
∴四边形ABED为平行四边形,
∴AD∥BF,∠ADG=∠ABC,
∴∠ADG=∠DEF,
∴∠ABC=∠DEF=∠ADG,
∵∠AGE为△ADG的外角,
∴∠AGE=∠DAG+∠ADG=∠GAD+∠ABC
(2)解:AG⊥DE,理由为:
由平移的性质得到∠EDF=∠BAC,
∵∠EDF=∠DAG,
∴∠BAC=∠DAG,
∵AB∥DE,
∴∠ABC+∠BEG=180°,
∵∠CAG+∠CEG=180°,
∴∠ABC=∠CAG,
∵MN∥BC,∴∠ABC=∠MAB,
∴∠MAB=∠CAG,
∵∠MAB+∠BAC+∠CAG+∠DAG=180°,
∴∠CAG+∠BAC=90°,即∠BAG=90°,
∵AB∥DE,
∴∠BAG+∠AGD=90°,
则AG⊥DE.
【解析】(1)利用平移的性质得到AB与DE平行且相等,得到四边形ABED为平行四边形,利用平行四边形的性质得到对角相等,利用外角性质即可得证;(2)AG垂直与DE,理由为:由平移的性质得到∠EDF=∠BAC,根据∠EDF=∠DAG,等量代换得到∠BAC=∠DAG,由AB与DE平行,利用两直线平行同旁内角互补得到一对角互补,等量代换得到∠ABC=∠CAG,利用等式的性质及平行线的性质即可得证.
【考点精析】解答此题的关键在于理解平行线的判定与性质的相关知识,掌握由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质,以及对多边形内角与外角的理解,了解多边形的内角和定理:n边形的内角和等于(n-2)180°.多边形的外角和定理:任意多边形的外角和等于360°.