��Ŀ����
����Ŀ������OABC��ֱ������ϵ�е�λ����ͼ��ʾ��A��C���������ֱ�ΪA��10��0����C��0��3����ֱ�� ![]() ��BC�ཻ�ڵ�D��������y=ax2+bx����A��D���㣮
��BC�ཻ�ڵ�D��������y=ax2+bx����A��D���㣮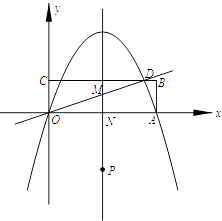
��1���������ߵĽ���ʽ��
��2������AD�����жϡ�OAD����״����˵�����ɣ�
��3������P�������ߵĶԳ����ϵ�һ�����㣬�Գ�����OD��x��ֱ��ڵ�M��N���ʣ��Ƿ���ڵ�P��ʹ���Ե�P��O��MΪ��������������OAD���ƣ������ڣ��������P�����ꣻ�������ڣ���˵�����ɣ�
���𰸡�
��1��
�⣺������ã���D��������Ϊ3��
�ߵ�D��ֱ��y= ![]() x�ϣ�
x�ϣ�
���D��������9��3����
����D��9��3������A��10��0�����������߿ɵã� ![]() ��
��
��ã�  ��
��
�������ߵĽ���ʽΪ��y=�� ![]() x2+
x2+ ![]() x��
x��
��2��
�⣺�ߵ�D����Ϊ��9��3������A����Ϊ��10��0����
��OA=10��OD= ![]() =3
=3 ![]() ��AD=
��AD= ![]() =
= ![]() ��
��
�Ӷ��ɵ�OA2=OD2+AD2��
�ʿ��жϡ�OAD��ֱ�������Σ�
��3��
�⣺����ͼ�οɵõ���P�͵�N�غ�ʱ�������OPM�ס�ODA��
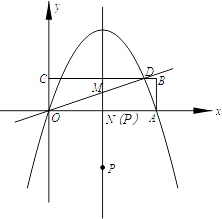
��ʱ��POM=��DOA����OPM=��ODA��
�ʿɵá�OPM�ס�ODA��OP= ![]() OA=5��
OA=5��
���ɵô�ʱ��P������Ϊ��5��0����
�ڹ���O��OD�Ĵ��߽��Գ����ڵ�P�䣬��ʱҲ�������P��OM�ס�ODA��
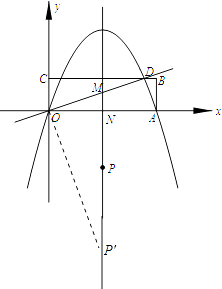
������ɵã���M�ĺ�����Ϊ5������ֱ�߷��̿ɵõ�M��������Ϊ ![]() ��
��
�ʿ����OM= ![]() ��
��
�ߡ�OP��M+��OMN=��DOA+��OMN=90�㣬
���OP��M=��DOA��
���P��OM�ס�ODA��
�ʿɵ� ![]() =
= ![]() ����
���� ![]() =
= ![]() ��
��
��ã�MP��= ![]() ��
��
�֡�MN=��M��������= ![]() ��
��
��P��N= ![]() ��
�� ![]() =15��
=15��
���ɵô�ʱ��P�������Ϊ��5����15����
���Ͽɵô��������ĵ�P����P������Ϊ��5��0����5����15����
����������1����������ɵó���D��������Ϊ3������ֱ�߽���ʽ�ɵó���D�ĺ����꣬�Ӷ�����D�͵�A���������ɵó������ߵĽ���ʽ����2���ֱ����OA��OD��AD�ij��ȣ��̶����ݹ��ɶ������涨�����жϳ���OAD��ֱ�������Σ���3������ͼ�οɵõ���P�͵�N�غ�ʱ�������OPM�ס�ODA���ڹ���O��OD�Ĵ��߽��Գ����ڵ�P�䣬��ʱҲ�������P��OM�ס�ODA���������Ƶ����ʷֱ�ó���P�����꼴�ɣ�
�����㾫�������ö��κ�����ͼ��Ͷ��κ��������ʶ���Ŀ�����жϼ��ɵõ��𰸣���Ҫ��֪���κ���ͼ��ؼ��㣺1�����ڷ���2���Գ��� 3������ 4����x�ύ�� 5����y�ύ�㣻�����ԣ���a>0ʱ���Գ�����ߣ�y��x�������С���Գ����ұߣ�y��x���������a<0ʱ���Գ�����ߣ�y��x��������Գ����ұߣ�y��x�������С��