题目内容
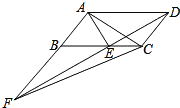
【题目】如图,平行四边形ABCD中,AE平分∠BAD,交BC于点E,且AB=AE,延长AB与DE的延长线交于点F.下列结论中:①△ABC≌△AED;②△ABE是等边三角形;③AD=AF;④S△ABE=S△CDE;⑤S△ABE=S△CEF.其中正确的是_____.
【答案】①②⑤
【解析】
由平行四边形的性质得出AD∥BC,AD=BC,由AE平分∠BAD,可得∠BAE=∠DAE,可得∠BAE=∠BEA,得AB=BE,由AB=AE,得到△ABE是等边三角形,②正确;则∠ABE=∠EAD=60°,由SAS证明△ABC≌△EAD,①正确;由△FCD与△ABD等底(AB=CD)等高(AB与CD间的距离相等),得出S△FCD=S△ABD,由△AEC与△DEC同底等高,所以S△AEC=S△DEC,得出S△ABE=S△CEF.⑤正确.
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴∠EAD=∠AEB,
又∵AE平分∠BAD,
∴∠BAE=∠DAE,
∴∠BAE=∠BEA,
∴AB=BE,
∵AB=AE,
∴△ABE是等边三角形;
②正确;
∴∠ABE=∠EAD=60°,
∵AB=AE,BC=AD,
∴△ABC≌△EAD(SAS);
①正确;
∵△FCD与△ABC等底(AB=CD)等高(AB与CD间的距离相等),
∴S△FCD=S△ABC,
又∵△AEC与△DEC同底等高,
∴S△AEC=S△DEC,
∴S△ABE=S△CEF;
⑤正确.
若AD与AF相等,即∠AFD=∠ADF=∠DEC,
即EC=CD=BE,
即BC=2CD,
题中未限定这一条件,
∴③④不一定正确;
故答案为:①②⑤.

 阅读快车系列答案
阅读快车系列答案【题目】为了提高学生书写汉字的能力,增强保护汉字的意识,某市举办了首届“汉字听写大赛”,经选拔后有50名学生参加决赛,这50名学生同时听写50个汉字,若每正确听写出一个汉字得1分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如下:
组别 | 成绩x分 | 频数(人数) |
第1组 | 25≤x<30 | 4 |
第2组 | 30≤x<35 | 8 |
第3组 | 35≤x<40 | 16 |
第4组 | 40≤x<45 | a |
第5组 | 45≤x<50 | 10 |
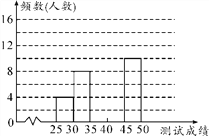
请结合图表完成下列各题:
(1)求表中a的值;
(2)请把频数分布直方图补充完整;
(3)若测试成绩不低于40分为优秀,则本次测试的优秀率是多少?
(4)第5组10名同学中,有4名男同学,现将这10名同学平均分成两组进行对抗练习,且4名男同学每组分两人,求小宇与小强两名男同学能分在同一组的概率.