��Ŀ����
����Ŀ��Ϊ���˽�ij�ֵ綯���������ܣ�ij���������ֵ綯�������г�죬�����ͼ�в�������ͳ��ͼ������![]() ��
��![]() ��
��![]() ��
��![]() ��ʾ һ�γ�����ʻ��������ֱ�Ϊ
��ʾ һ�γ�����ʻ��������ֱ�Ϊ![]() ��
��![]() ��
��![]() ��
��![]() .
.
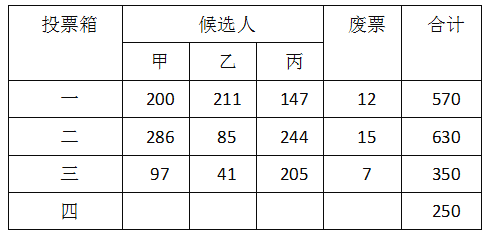
��1������α����ĵ綯�������м���������ȫ����ͳ��ͼ��
�綯����һ�γ�����ʻ�����������ͳ��ͼ
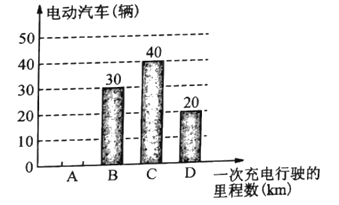
�綯����һ�γ�����ʻ�����������ͳ��ͼ
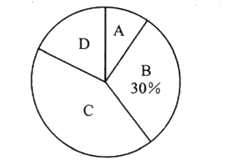
��2��������ͳ��ͼ�б�ʾһ�γ�����ʻ·Ϊ![]() ������Բ�ĽǵĶ�����
������Բ�ĽǵĶ�����
��3���������ֵ綯����һ�γ�����ʻ��ƽ����̶���![]() ��
��
���𰸡���1���ܹ���![]() ��.
��.![]() ����10����ͼ�ԣ���2��72�㣻��3�����ֵ綯����һ�γ�����ʻ��ƽ�������Ϊ
����10����ͼ�ԣ���2��72�㣻��3�����ֵ綯����һ�γ�����ʻ��ƽ�������Ϊ![]() ǧ��.
ǧ��.
��������
��1����������ͳ��ͼ������ͼ��֪����һ�γ�����ʻ���������ΪB�ȼ�����30���綯��������ռ�İٷֱ�Ϊ30%����30��30%���������α����ĵ綯�����������ٷֱ��ȥB��C��D�ȼ����������õ�A�ȼ������������ɲ�ȫ����ͼ��
��2����D�ȼ����������������������õ�����ռ�İٷֱȣ��ٳ���360���õ�����Բ�ĽǵĶ�����
��3��������̳������������������ɽ��
�⣺��1����α����ĵ綯��������30��30%=100��������
A�ȼ���������Ϊ��100-��30+40+20��=10��������
����ͼ�������£�

��2��D�ȼ���Ӧ��Բ�ĽǶ���Ϊ![]() .
.
��3��![]() .
.
�����ֵ綯����һ�γ�����ʻ��ƽ�������Ϊ![]() ǧ��.
ǧ��.