题目内容
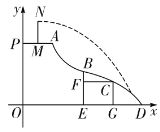
【题目】如图,已知△ABC内接于⊙O,BC为⊙O直径,延长AC至D,过D作⊙O切线,切点为E,且∠D=90°,连接BE.DE=12,
(1)若CD=4,求⊙O的半径;
(2)若AD+CD=30,求AC的长.

【答案】(1)20;(2)18.
【解析】
(1) (2) 连接OE,作OH⊥AD于H,利用切线性质和垂径定理、矩形的判定和性质、勾股定理即可解答;
(1)解:连接OE,作OH⊥AD于H,
∵DE是⊙O的切线,
∴OE⊥DE.
又∵∠D=90°,
∴四边形OHDE是矩形,
设⊙O的半径为r,
在Rt△OCH中,
OC2=CH2+OH2,
∴r2=(r﹣4)2+144,
∴半径r=20.
(2)解:∵OH⊥AD,
∴AH=CH.
又∵AD+CD=30,即:(AH+HD)+(HD﹣CH)=30.
∴2HD=30,HD=15,即OE=HD=OC=15,
∴在Rt△OCH中,CH=![]() =
=![]() =9.
=9.
∴AC=2CH=18.

 特高级教师点拨系列答案
特高级教师点拨系列答案【题目】某商场用两个月时间试销某种新型商品,经市场调查,该商品的第![]() 天的进价
天的进价![]() (元/件)与
(元/件)与![]() (天)之间的相关信息如下表:
(天)之间的相关信息如下表:
时间 |
|
|
进价 |
| 40 |
该商品在销售过程中,销售量![]() (件)与
(件)与![]() (天)之间的函数关系如图所示:
(天)之间的函数关系如图所示:
在销售过程中,商场每天销售的该产品以每件80元的价格全部售出.
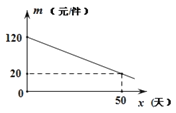
(1)求该商品的销售量![]() (件)与
(件)与![]() (天)之间的函数关系;
(天)之间的函数关系;
(2)设第![]() 天该商场销售该商品获得的利润为
天该商场销售该商品获得的利润为![]() 元,求出
元,求出![]() 与
与![]() 之间的函数关系式,并求出第几天销售利润最大,最大利润是多少元?
之间的函数关系式,并求出第几天销售利润最大,最大利润是多少元?
(3)在销售过程中,当天的销售利润不低于2400元的共有多少天?
【题目】为弘扬中华优秀传统文化,某校组织了“古诗词”知识竞赛,由九年级的若干名学生参加选拔赛,从中选出10名优胜者,下面是对参赛学生成绩的不完整统计.
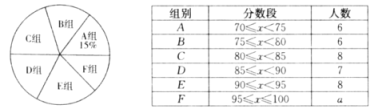
(1)统计表中,![]() =_____;各组人数的中位数是_____;统计图中,
=_____;各组人数的中位数是_____;统计图中,![]() 组所在扇形的圆心角是_____°;
组所在扇形的圆心角是_____°;
(2)李明同学得了88分,他说自己在参加选拔赛的同学中属于中午偏上水平,你认为他说的有道理吗?为什么?
(3)选出的10名优胜者中,男生、女生的分布情况如下表.
一班 | 二班 | 三班 | 四班 | 五班 | 六班 | |
男生人数 | 1 | 1 | 2 | 1 | 0 | 0 |
女生人数 | 1 | 0 | 0 | 2 | 1 | 1 |
若从中任选1名男生和1名女生代表学校参加全区的比赛,请有列表法或画树状图法求男生和女生都出在四班的概率.