Question

如图，矩形ABCD中，AB=20，BC=10，点P为AB边上一动点，DP交AC于点Q.
（1）求证：△APQ∽△CDQ；
（2）P点从A点出发沿AB边以每秒1个单位的速度向B点移动，移动时间为t秒.
①当t为何值时，DP⊥AC？
②设，写出y与t之间的函数解析式，并探究P点运动到第几秒到第几秒之间时，y取得最小值.

Answer 1

（1）证明见解析；（2）①5；②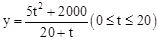，8-9.

解析试题分析：（1）如图，由矩形的性质求出∠1=∠2，∠3=∠4即可证明△APQ∽△CDQ.
（2）①当DP⊥AC时，由△ADC∽△PAD列比例式可求解.
②根据相似，求出两个三角形的高（用t的代数式表示），即可求出y与t之间的函数解析式；列表求出函数值得出P点运动到第8秒到第9秒之间时，y取得最小值.
试题解析：（1）如图，∵四边形ABCD是矩形，∴AB∥CD. ∴∠1=∠2，∠3=∠4.
∴△APQ∽△CDQ.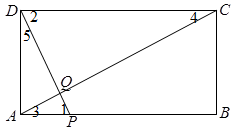

（2）①当DP⊥AC时，∴∠4+∠2=90 ^o.
又∵∠5+∠2=90 ^o，∴∠4=∠5.
又∵∠ADC=∠DAP=90 ^o，∴△ADC∽△PAD.∴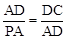，即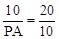.∴PA=5.
∵P点从A点出发沿AB边以每秒1个单位的速度向B点移动，∴t=5.
②设△APQ的边AP上的高为h，则△DCQ的边上的高为.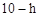
∵由（1）△APQ∽△CDQ，∴.∴.∴.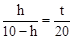
∴，.
∴.
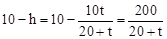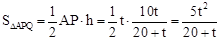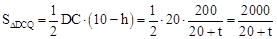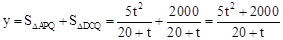∴y与t之间的函数解析式为.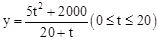
给出t的部分取值，计算出y的对应值列表如下：

t	0	1	2	3	4	5	6	7	8	9	10
y	100	95.48	91.88	88.91	86.67	85	83.85	83.15	82.86	82.93	83.33
t	11