题目内容
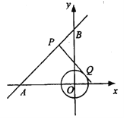
【题目】如图，在平面直角坐标系xOy中，直线AB经过点A（－4，0）、B（0，4），⊙O的半径为1（O为坐标原点），点P在直线AB 上，过点P作⊙O的一条切线PQ，Q为切点，则切线长PQ的最小值为（ ）．
A．
B．
C．2
D．3
【答案】B.
【解析】
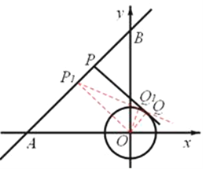
试题分析：如图，过点O作OP 1 ⊥AB，过点P 1 作⊙O的切线交⊙O于点Q 1 ，连接OQ，OQ 1 .当PQ⊥AB时，易得四边形P 1 PQO是矩形，即PQ=P 1 O.∵P 1 Q 1 是⊙O的切线， ∴∠OQ 1 P 1 =90 0 .∴在Rt△OP 1 Q 1 中，P 1 Q 1 ＜P 1 O，∴P 1 Q 1 即是切线长PQ的最小值.∵A（－4，0），B（0，4），∴OA=OB=4.∴△OAB是等腰直角三角形. ∴△AOP 1 是等腰直角三角形.根据勾股定理，得OP 1 =2
.∵⊙O的半径为1，∴OQ 1 =1.根据勾股定理，得P 1 Q 1 =
.故选B．
练习册系列答案
相关题目
