题目内容
【题目】甲、乙两台机器共同加工一批零件,在加工过程中两台机器均改变了一次工作效率.从工作开始到加工完这批零件两台机器恰好同时工作6小时.甲、乙两台机器各自加工的零件个数y(个)与加工时间x(时)之间的函数图象分别为折线OA﹣AB与折线OC﹣CD.如图所示.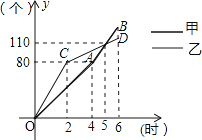
(1)求甲机器改变工作效率前每小时加工零件的个数.
(2)求乙机器改变工作效率后y与x之间的函数关系式.
(3)求这批零件的总个数.
【答案】
(1)
解:80÷4=20(件);
(2)
解:∵图象过C(2,80),D(5,110),
∴设解析式为y=kx+b(k≠0),
∴![]() ,解得:
,解得:![]() ,
,
∴y乙=10x+60(2≤x≤6);
(3)
解:∵AB过(4,80),(5,110),
∴设AB的解析式为y甲=mx+n(m≠0),
∴![]() ,解得:
,解得:![]() ,
,
∴y甲=30x﹣40(4≤x≤6),
当x=6时,y甲=30×6﹣40=140,y乙=10×6+60=120,
∴这批零件的总个数是140+120=260.
【解析】(1)甲改变工作效率前的工作效率为改变前加工的总件数,除以加工的总时间即可;
(2)利用待定系数法求一次函数解析式即可;
(3)利用函数解析式求出甲、乙两机器6小时加工的总件数,求其和即可.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某学校举行一次体育测试,从所有参加测试的中学生中随机的抽取10名学生的成绩,制作出如下统计表和条形图,请解答下列问题:
编号 | 成绩 | 等级 | 编号 | 成绩 | 等级 |
① | 95 | A | ⑥ | 76 | B |
② | 78 | B | ⑦ | 85 | A |
③ | 72 | C | ⑧ | 82 | B |
④ | 79 | B | ⑨ | 77 | B |
⑤ | 92 | A | ⑩ | 69 | C |

(1)孔明同学这次测试的成绩是87分,则他的成绩等级是 等;
(2)请将条形统计图补充完整;
(3)已知该校所有参加这次测试的学生中,有60名学生成绩是A等,请根据以上抽样结果,估计该校参加这次测试的学生总人数是多少人.



